Question

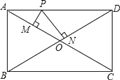
【题目】如图，矩形ABCD中，对角线AC与BD相交于点O，P为AD上的动点，过点P作PM⊥AC，PN⊥BD，垂足分别为M、N，若AB=m，BC=n，则PM+PN=（　　）

A.B.C.D.

Answer 1

【答案】C

【解析】

连接OP，由矩形的性质得出OA=OD，∠ABC=90°，由勾股定理求出AC，得出OA，由△OAP的面积+△ODP的面积=矩形ABCD的面积，即可得出结果．

连接OP，如图所示：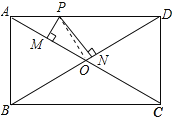

∵四边形ABCD是矩形，

∴∠ABC=90°，OA=AC，OD=BD，AC=BD，

∴OA=OD，AC=，

∴OA=OD=，

∵△OAP的面积+△ODP的面积=△AOD的面积=矩形ABCD的面积，

即OAPM+ODPN=OA（PM+PN）=ABBC=mn，

∴PM+PN=，

故选：C．