Question

已知，△ABC与△DEF中，∠C=∠F=90°，∠A=∠D，BC=6，AC=8，△DEF的周长为72，求△DEF各边的长．

Answer 1

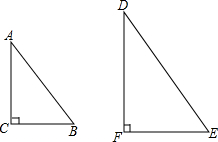解：∵∠C=∠F=90°，∠A=∠D，
∴△ACB∽△DFE，
∴==，
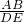∵BC=6，AC=8，
∴AB==10，
∴△ABC的周长为6+8+10=24，
∵△DEF的周长为72，
∴两三角形△ABC与△DEF的相似之比为：=，
∴===，
∴===，
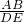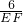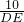∴DF=24，EF=18，DE=30．
分析：利用相似三角形的判定得出△ACB∽△DFE，再利用勾股定理得出AB=10，利用△ABC的周长为6+8+10=24，以及△DEF的周长为72，进而得出两三角形△ABC与△DEF的相似之比即可得出答案．
点评：此题主要考查了相似三角形的判定与性质，根据已知得出两三角形△ABC与△DEF的周长之比是解题关键．