题目内容
 由于保管不慎,小明把一道数学题染上了污渍,变成了“如图,在△ABC中∠A=30°,tanB=
由于保管不慎,小明把一道数学题染上了污渍,变成了“如图,在△ABC中∠A=30°,tanB= ,AC=4
,AC=4| 3 |
分析:作辅助线CH⊥AB于H.Rt△ACH中,利用正弦函数求得CH=2
、利用余弦定理求得AH=6,所以BH=AB-AH=4;然后根据直角三角形的正切函数值求得tanB=
=
.
| 3 |
| CH |
| BH |
| ||
| 2 |
解答: 解:作CH⊥AB于H,
解:作CH⊥AB于H,
Rt△ACH中,
CH=AC•sinA,
=4
×sin30°,
=2
,
AH=AC•cosA,
=4
×cos30°,
=6,
∴BH=AB-AH=4,
∴tanB=
=
,
∴污渍部分内容内为
.
 解:作CH⊥AB于H,
解:作CH⊥AB于H,Rt△ACH中,
CH=AC•sinA,
=4
| 3 |
=2
| 3 |
AH=AC•cosA,
=4
| 3 |
=6,
∴BH=AB-AH=4,
∴tanB=
| CH |
| BH |
| ||
| 2 |
∴污渍部分内容内为
| ||
| 2 |
点评:本题考查了解直角三角形.解题时,通过作辅助线CH⊥AB于H构建△ACH,然后根据直角三角形的三角函数的定义解答∠B的正切值.

练习册系列答案
 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案
相关题目
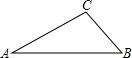 由于保管不慎,小明把一道数学题染上了污渍,变成了“如图,在△ABC中∠A=30°,tanB=
由于保管不慎,小明把一道数学题染上了污渍,变成了“如图,在△ABC中∠A=30°,tanB=
 ,AC=
,AC= ,求AB的长”.这时小明去翻看了标准答案,显示AB=10.你能否帮助小明通过计算说明污渍部分的内容是什么?
,求AB的长”.这时小明去翻看了标准答案,显示AB=10.你能否帮助小明通过计算说明污渍部分的内容是什么?
