Question

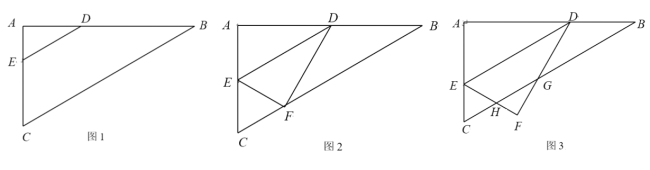
【题目】已知：如图1，在中，，∠ABC=30°，，点、E分别是边、AC上动点，点不与点、重合，DE∥BC．

（1）如图1，当AE=1时，求长；

（2）如图2，把沿着直线翻折得到，设

①当点F落在斜边上时，求的值；

② 如图3，当点F落在外部时，EF、DF分别与相交于点H、G，如果△ABC和△DEF重叠部分的面积为，求与的函数关系式及定义域．（直接写出答案）

Answer 1

【答案】（1）BD=；（2）①x=2；②.

【解析】

（1）根据DE∥BC，可得∠ADE=30°，然后分别利用三角函数求出AB和AD即可；

（2）①设，则AE=EF=4－x，然后证明△CEF是等边三角形即可解决问题；

②由①可知CE=x，AE=EF=4－x，△CEF是等边三角形，然后分别求出HF、FG和AD，利用三角形面积公式计算出和，进而得到，然后根据列式整理，并求出定义域即可.

解：（1）∵，∠ABC=30°，，AE=1，

∴，

∵DE∥BC，

∴∠ADE=30°，

∴，

∴BD=AB－AD=；

（2）①设，则AE=4－x，

∴EF=4－x，

∵∠ADE=∠B =30°，

∴∠AED=∠C =60°，

∴∠CEF=180°－60°－60°=60°，

∴△CEF是等边三角形，

∴CE=EF，即x=4-x，

∴x=2；

②由①可知CE=x，AE=EF=4－x，△CEF是等边三角形，

∴HF=EF－EH=4－x－x=4－2x，∠FHG=∠CHE=60°，

∵∠F=∠A=90°，

∴FG=HF=，

∴，

∵AE= 4－x，∠ADE=30°，

∴，

∴，

∴，

∴，

∵当x=2时，点F落在斜边上，

∴定义域为：，

即.