题目内容
用换元法解方程
时，设y=
，则原方程可化为关于y的整式方程是________．
6y2-3y-1=0
分析：设y=，则原方程可化为关于y的分式方程：2y-
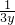=1，然后去分母得到6y2-1=3y，再进行整理即可．
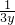解答：设y=，则原方程可化为：2y-=1，
方程两边乘以3y得6y2-1=3y，
整理得得6y2-3y-1=0．
故答案为6y2-3y-1=0．
点评：本题考查了换元法解分式方程：当分式方程中含未知数的式子整体保持不变时，可以一个字母表示这个式子，这样分式方程就可化为简单的分式方程或整式方程，然后再解简单的分式方程或整式方程，这种方程叫换元法．
分析：设y=
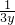，则原方程可化为关于y的分式方程：2y-=1，然后去分母得到6y2-1=3y，再进行整理即可．解答：设y=
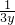，则原方程可化为：2y-=1，方程两边乘以3y得6y2-1=3y，
整理得得6y2-3y-1=0．
故答案为6y2-3y-1=0．
点评：本题考查了换元法解分式方程：当分式方程中含未知数的式子整体保持不变时，可以一个字母表示这个式子，这样分式方程就可化为简单的分式方程或整式方程，然后再解简单的分式方程或整式方程，这种方程叫换元法．
练习册系列答案
相关题目
时，设
，则原方程可化为
B、
C、
D、
时，设
=y，则原方程化为关于y的方程是 ．
时，设y=x2-3x，则原方程可化为（ ）
时，设
，则原方程化为关于y的方程是 ．
时，设
，则原方程化为关于y的方程是（ ）