题目内容
【题目】如图，在平面直角坐标系
中，矩形
的对角线
与
交于点
，点
的坐标为
，
轴于点
，反比例函数
的图象经过点
．
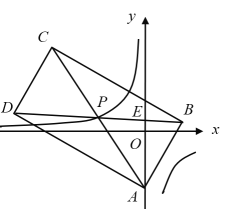
（1）求
的值；
（2）若将矩形向下平移
个单位，使点
落在反比例函数的图象上，求的值；
（3）求
的值．
【答案】（1）
；（2）
；（3）
．
【解析】
（1）根据待定系数法将把点
代入
即可求出
的值；
（2）在
中，由勾股定理可计算
的长，根据矩形性质可知
，从而求出B点坐标，再由反比例函数求出矩形向下平移后对应点坐标即可解答；
（3）由矩形性质可知
，
，根据（2）可得D点坐标，在
中求出
即可．
解：（1）把点代入，得
．
解得
．
（2）∵，
，
轴于点
．
∴
，
，
．
由勾股定理，得
∵四边形
是矩形，
∴
．
∴点
的横坐标为
，
由，知反比例函数的解析式为
当
时，
，
∴下移的距离
．
（3）∵四边形是矩形，
∴，，
∴点
的横坐标为:
，
∴
．
∵
，
，
∴
，
，
由勾股定理，得
．
∴
．
练习册系列答案
相关题目
【题目】某书店为了迎接“读书节”制定了活动计划，以下是活动计划书的部分信息：
“读书节”活动计划书 | ||
书本类别 | A类 | B类 |
进价(单位：元) | 18 | 12 |
备注 | 1.用不超过16800元购进A，B两类图书共1000本； 2．A类图书不少于600本； …… |
(1)陈经理查看计划数时发现：A类图书的标价是B类图书标价的1.5倍，若顾客用540元购买图书，能单独购买A类图书的数量恰好比单独购买B类图书的数量少10本，请求出A，B两类图书的标价；
(2)经市场调查后，陈经理发现他们高估了“读书节”对图书销售的影响，便调整了销售方案，A类图书每本标价降低a元(0＜a＜5)销售，B类图书价格不变，那么书店应如何进货才能获得最大利润？
