题目内容
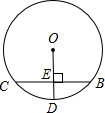
如图，BC是⊙O的弦，OD⊥BC于E，交
于D
（1）若BC=8，ED=2，求⊙O的半径．
（2）画出直径AB，连接AC，观察所得图形，请你写出两个新的正确结论：______；______．
 |
| BC |
（1）若BC=8，ED=2，求⊙O的半径．
（2）画出直径AB，连接AC，观察所得图形，请你写出两个新的正确结论：______；______．
（1）连接OB
∵OD⊥BC，BC=8
∴BE=CE=
BC=4（1分）
设⊙O的半径为R，则OE=OD-DE=R-2
在Rt△OEB中，由勾股定理得
OE2+BE2=OB2，即（R-2）2+42=R2（2分）
解得R=5（3分）
∴⊙O的半径为5；
（2）AC⊥CB，AC∥OD，OE=
AC等．（5分）
注：写对一个结论给（1分）．
∵OD⊥BC，BC=8
∴BE=CE=
| 1 |
| 2 |
设⊙O的半径为R，则OE=OD-DE=R-2
在Rt△OEB中，由勾股定理得
OE2+BE2=OB2，即（R-2）2+42=R2（2分）
解得R=5（3分）
∴⊙O的半径为5；
（2）AC⊥CB，AC∥OD，OE=
| 1 |
| 2 |
注：写对一个结论给（1分）．
练习册系列答案
教学练新同步练习系列答案
课前课后同步练习系列答案
相关题目
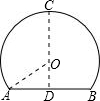
∠EPF的两边相交于A、B和C、D，连接OA，此时有OA
