题目内容
如图,在同一平面内,将两个全等的等腰直角三角形ABC和ADE摆放在一起,A为公共顶点,∠BAC=∠ADE=90°,它们的斜边长为2,若△ABC固定不动,△ADE绕点A旋转,AE、AD与边BC的交点分别为F、G (点F不与点C重合,点G不与点B重合),设BF=a,CG=b.(1)请在图(1)中找出两对相似但不全等的三角形,并选取其中一对进行证明.
(2)求b与a的函数关系式,直接写出自变量a的取值范围.
(3)以△ABC的斜边BC所在的直线为x轴,BC边上的高所在的直线为y轴,建立平面直角坐标系(如图2).若BG=CF,求出点G的坐标,猜想线段BG、FG和CF之间的关系,并通过计算加以验证.

分析:(1)找到有公共角的和45°角的两个三角形即可;
(2)易得△ACG∽△FBA,利用相似三角形的对应边成比例可得b与a的函数关系式,根据点F与点C重合时a为1,点G与点B重合时,a为2可得a的取值;
(3)结合(3)的条件和(2)的结论可得a,b的值,进而计算可得G、F的坐标,分别表示出BG、FG和CF的长度,看有什么等量关系即可.
(2)易得△ACG∽△FBA,利用相似三角形的对应边成比例可得b与a的函数关系式,根据点F与点C重合时a为1,点G与点B重合时,a为2可得a的取值;
(3)结合(3)的条件和(2)的结论可得a,b的值,进而计算可得G、F的坐标,分别表示出BG、FG和CF的长度,看有什么等量关系即可.
解答: 解:(1)△ACG∽△FAG,△FAG∽△FBA.
解:(1)△ACG∽△FAG,△FAG∽△FBA.
∵∠GAF=∠C=45°,
∠AGF=∠AGC,
∴△ACG∽△FAG.类似证明△FAG∽△FBA;
(2)∵∠CAG=∠CAF+45°,∠BFA=∠CAF+45°,
∴∠CAG=∠BFA.
∵∠B=∠C=45°,
∴△ACG∽△FBA,
∴
=
.
由题意可得CA=BA=
.
∴
=
.∴b=
.
自变量a的取值范围为1<a<2.
(3)由BG=CF可得BF=CG,即a=b.
∵b=
,
∴a=b=
.
∵OB=OC=
BC=1,
∴OF=OG=
-1.
∴G(1-
,0).
线段BG、FG和CF之间的关系为BG2+CF2=FG2;
∵BG=OB-OG=1-(
-1)=2-
=CF,
FG=BC-2BG=2-2(2-
)=2
-2.
∵BG2+CF2=2BG2=2(2-
)2=12-8
,FG2=(2
-2)2=12-8
.
∴BG2+CF2=FG2.
 解:(1)△ACG∽△FAG,△FAG∽△FBA.
解:(1)△ACG∽△FAG,△FAG∽△FBA.∵∠GAF=∠C=45°,
∠AGF=∠AGC,
∴△ACG∽△FAG.类似证明△FAG∽△FBA;
(2)∵∠CAG=∠CAF+45°,∠BFA=∠CAF+45°,
∴∠CAG=∠BFA.
∵∠B=∠C=45°,
∴△ACG∽△FBA,
∴
| CG |
| BA |
| CA |
| FB |
由题意可得CA=BA=
| 2 |
∴
| b | ||
|
| ||
| a |
| 2 |
| a |
自变量a的取值范围为1<a<2.
(3)由BG=CF可得BF=CG,即a=b.
∵b=
| 2 |
| a |
∴a=b=
| 2 |
∵OB=OC=
| 1 |
| 2 |
∴OF=OG=
| 2 |
∴G(1-
| 2 |
线段BG、FG和CF之间的关系为BG2+CF2=FG2;
∵BG=OB-OG=1-(
| 2 |
| 2 |
FG=BC-2BG=2-2(2-
| 2 |
| 2 |
∵BG2+CF2=2BG2=2(2-
| 2 |
| 2 |
| 2 |
| 2 |
∴BG2+CF2=FG2.
点评:综合考查了相似三角形的判定与性质;利用两角对应相等得到所需的两三角形相似进而得到对应边的比成比例是解决本题的关键.

练习册系列答案
相关题目
 20、如图,在同一平面内,有三条直线a、b、c,且a∥b,如果直线a与c交于点O,那么直线c与b的位置关系是
20、如图,在同一平面内,有三条直线a、b、c,且a∥b,如果直线a与c交于点O,那么直线c与b的位置关系是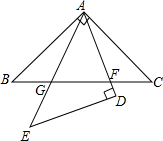 如图,在同一平面内,将两个全等的等腰直角三角形ABC和ADE摆放在一起,A为公共顶点,∠BAC=∠ADE=90°,若△ABC固定不动,△ADE绕点A旋转,AD、AE与边BC的交点分别为F、G(点G不与点B重合,点F不与点C重合).
如图,在同一平面内,将两个全等的等腰直角三角形ABC和ADE摆放在一起,A为公共顶点,∠BAC=∠ADE=90°,若△ABC固定不动,△ADE绕点A旋转,AD、AE与边BC的交点分别为F、G(点G不与点B重合,点F不与点C重合).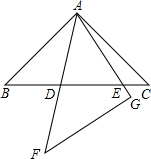 点分别为D、E(点D不与点B重合,点E不与点C重合),设BE=m,CD=n.
点分别为D、E(点D不与点B重合,点E不与点C重合),设BE=m,CD=n. 按要求作图:
按要求作图: 如图,在同一平面内有A、B、C三个点,根据要求画图:
如图,在同一平面内有A、B、C三个点,根据要求画图: