题目内容
如图，AD⊥BC于D，CE⊥AB于E，交AD于F，则图中相似三角形的对数是（ ）分析：由AD⊥BC，CE⊥AB，可得∠AEF=∠ADC=∠BEC=∠ABD=90°，然后由∠A，∠B是公共角，∠AFE与∠CFD是公共角，可证得△AEF∽△CEF∽△ADB∽△CEB．
解答：解：∵AD⊥BC，CE⊥AB，
∴∠AEF=∠ADC=∠BEC=∠ABD=90°，
∵∠AFE=∠CFD，
∴△AFE∽△CFD，
∵∠B是公共角，
∴△ABD∽△CBE，
∵∠A是公共角，
∴△AEF∽△ADB，
∴△AEF∽△CEF∽△ADB∽△CEB．
∴图中相似三角形的对数是6对．
故选D．
∴∠AEF=∠ADC=∠BEC=∠ABD=90°，
∵∠AFE=∠CFD，
∴△AFE∽△CFD，
∵∠B是公共角，
∴△ABD∽△CBE，
∵∠A是公共角，
∴△AEF∽△ADB，
∴△AEF∽△CEF∽△ADB∽△CEB．
∴图中相似三角形的对数是6对．
故选D．
点评：此题考查了相似三角形的判定．此题难度适中，注意掌握数形结合思想的应用，小心别漏解．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
15、如图，AD⊥BC于D，DE∥AC，则∠C与∠ADE之和为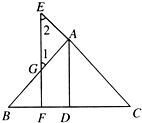
23、已知：如图，AD⊥BC于D，EF⊥BC于F，交AB于G，交CA延长线于E，∠1=∠2．
22、如图，AD⊥BC于D，EF⊥BC于F，且∠E=∠1，求证∠BAD=∠CAD．
23、如图，AD⊥BC于D，EF⊥BC于E，∠1=∠2，AB与DG平行吗？为什么？
（2013•义乌市）如图，AD⊥BC于点D，D为BC的中点，连接AB，∠ABC的平分线交AD于点O，连结OC，若∠AOC=125°，则∠ABC=