题目内容
已知关于 的一元二次方程
的一元二次方程 有两个不相等的实数根
有两个不相等的实数根
(1)求 的取值范围;
的取值范围;
(2)若 为正整数,且该方程的根都是整数,求
为正整数,且该方程的根都是整数,求 的值。
的值。
 的一元二次方程
的一元二次方程 有两个不相等的实数根
有两个不相等的实数根(1)求
 的取值范围;
的取值范围;(2)若
 为正整数,且该方程的根都是整数,求
为正整数,且该方程的根都是整数,求 的值。
的值。(1)k< (2)2
(2)2
 (2)2
(2)2解:(1)∵关于 的一元二次方程
的一元二次方程 有两个不相等的实数根,
有两个不相等的实数根,
∴ 。
。
解得:k< 。
。
(2)∵k为k< 的正整数,∴k=1或2。
的正整数,∴k=1或2。
当k=1时,方程为 ,两根为
,两根为 ,非整数,不合题意;
,非整数,不合题意;
当k=2时,方程为 ,两根为
,两根为 或
或 ,都是整数,符合题意。
,都是整数,符合题意。
∴k的值为2。
(1)根据方程有两个不相等的实数根,得到根的判别式的值大于0列出关于k的不等式,求出不等式的解集即可得到k的范围。
(2)找出k范围中的整数解确定出k的值,经检验即可得到满足题意k的值。
 的一元二次方程
的一元二次方程 有两个不相等的实数根,
有两个不相等的实数根,∴
 。
。解得:k<
 。
。(2)∵k为k<
 的正整数,∴k=1或2。
的正整数,∴k=1或2。当k=1时,方程为
 ,两根为
,两根为 ,非整数,不合题意;
,非整数,不合题意;当k=2时,方程为
 ,两根为
,两根为 或
或 ,都是整数,符合题意。
,都是整数,符合题意。∴k的值为2。
(1)根据方程有两个不相等的实数根,得到根的判别式的值大于0列出关于k的不等式,求出不等式的解集即可得到k的范围。
(2)找出k范围中的整数解确定出k的值,经检验即可得到满足题意k的值。

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 ,则△ABC的周长是 .
,则△ABC的周长是 .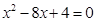 的两个根分别是a和b,则a+b=_______.
的两个根分别是a和b,则a+b=_______. 的解为 .
的解为 . 的根的情况是
的根的情况是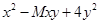 是一个完全平方式,那么
是一个完全平方式,那么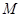 的值是( )
的值是( )
 则x与y关系是( )
则x与y关系是( ) (2)
(2) 

