Question

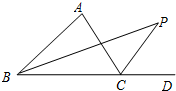如图，在△ABC中，∠ABC与外角∠ACD的平分线交于点P．请你从下列三个条件中选择一个作为已知条件，求∠P的度数．
条件（1）∠ABC=40°，∠ACD=120°；
条件（2）∠ABC=40°，∠A=80°；
条件（3）若∠A=α°．
说明：若选择条件（1）完成解答可得5分；
若选择条件（2）完成解答可得8分；
若选择条件（1）完成解答可得10分；
解：我选择的条件是______．

Answer 1

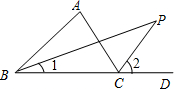选择的条件是（1）∠ABC=40°，∠ACD=120°；
解：∵BD平分∠ABC，
∴∠1=∠ABC=20°，
∵CP平分∠ACD，
∴∠2=∠ACD=60°，
∵∠2是△PBC的外角，
∴∠2=∠1+∠P，
∴∠P=∠2-∠1=60°-20°=40°．
答：∠P是40°；
故答案为：（1）∠ABC=40°，∠ACD=120°；

选择的条件是（2）∠ABC=40°，∠A=80°；
∵BD平分∠ABC，
∴∠1=∠ABC=20°，
∵∠ACD是△ABC的外角，
∴∠ACD=∠A+∠ABC=40°+80°=120°，
∵CP平分∠ACD，
∴∠2=∠ACD=60°，
∵∠2是△PBC的外角，
∴∠2=∠1+∠P，
∴∠P=∠2-∠1=60°-20°=40°．
答：∠P是40°；
选择的条件是（3）若∠A=α°．
∵BD平分∠ABC，
∴∠1=∠ABC，
∵∠ACD是△ABC的外角，
∴∠ACD=∠A+∠ABC，
∴∠ACD-∠ABC=∠A，
∵CP平分∠ACD，
∴∠2=∠ACD，
∵∠2是△PBC的外角，
∴∠2=∠1+∠P，
∴∠P=∠2-∠1=∠ACD-∠ABC=∠A=α°．
答：∠P是α．
分析：选择的条件是（1）∠ABC=40°，∠ACD=120°；由BD平分∠ABC，可知∠1=∠ABC，再由CP平分∠ACD，
可知∠2=∠ACD，由∠2是△PBC的外角可知∠2=∠1+∠P，故∠P=∠2-∠1．
点评：本题考查的是三角形内角和定理及三角形外角的性质，熟知三角形的外角等于与之不相邻的两个内角的和是解答此题的关键．