题目内容
（2000•陕西）如图，在矩形ABCD中，EF是BD的垂直平分线，已知BD=20，EF=15，求矩形ABCD的周长．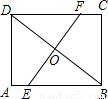
【答案】分析：设长AB=x，宽BC=y，根据题意可证Rt△DAB∽Rt△EOB，于是有∴
，又因为AD=BC，DF=BE，即
，解得x、y的值，即可求矩形周长．
解答：解：设长AB=x，宽BC=y，
∵∠DAB=90°=∠EOB=90°，∠B=∠B，
∴Rt△DAB∽Rt△EOB，
∴
，
∵AD=BC，DF=BE，
∴
，（5分）
解得
，
（舍去），（7分）
∴矩形周长为56．（8分）
点评：本题考查了相似三角形的判定和性质，线段垂直平分线以及矩形的性质等知识点，
，又因为AD=BC，DF=BE，即，解得x、y的值，即可求矩形周长．解答：解：设长AB=x，宽BC=y，
∵∠DAB=90°=∠EOB=90°，∠B=∠B，
∴Rt△DAB∽Rt△EOB，
∴
，∵AD=BC，DF=BE，
∴
，（5分）解得
，（舍去），（7分）∴矩形周长为56．（8分）
点评：本题考查了相似三角形的判定和性质，线段垂直平分线以及矩形的性质等知识点，
练习册系列答案
芒果教辅达标测试卷系列答案
相关题目
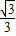x+2
上，求此抛物线的解析式；
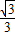x+2
上，求此抛物线的解析式；
