题目内容
 某校九年级的一场篮球比赛中,如图队员甲正在投篮,已知球出手时离地面高
某校九年级的一场篮球比赛中,如图队员甲正在投篮,已知球出手时离地面高| 20 | 9 |
(l)建立如图的平面直角坐标系,求出此轨迹所在抛物线的解析式.
(2)问此球能否准确投中?
分析:(1)根据抛物线的顶点坐标及球出手时的坐标,可确定抛物线的解析式;
(2)令x=7,求出y的值,与3m比较即可作出判断.
(2)令x=7,求出y的值,与3m比较即可作出判断.
解答:解:(1)由题意得,抛物线的顶点坐标为(4,4),球出手时的坐标为(0,
),
设抛物线解析式为:y=a(x-4)2+4,
将点(0,
)代入可得:16a+4=
,
解得:a=-
,
则抛物线的解析式为:y=-
(x-4)2+4;
(2)令x=7,则y=-
×9+4=3,
∵3m=3m,
∴此球能准确投中.
| 20 |
| 9 |
设抛物线解析式为:y=a(x-4)2+4,
将点(0,
| 20 |
| 9 |
| 20 |
| 9 |
解得:a=-
| 1 |
| 9 |
则抛物线的解析式为:y=-
| 1 |
| 9 |
(2)令x=7,则y=-
| 1 |
| 9 |
∵3m=3m,
∴此球能准确投中.
点评:本题考查了二次函数的应用,解答本题的关键是利用待定系数法求出抛物线解析式,注意建立数学模型,培养自己利用数学知识解决实际问题的能力.

练习册系列答案
相关题目
 某校九年级的一场篮球比赛中,如图队员甲正在投篮,已知球出手时离地面高
某校九年级的一场篮球比赛中,如图队员甲正在投篮,已知球出手时离地面高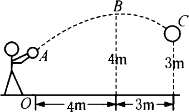
 某校九年级的一场篮球比赛中,如图队员甲正在投篮,已知球出手时离地面高
某校九年级的一场篮球比赛中,如图队员甲正在投篮,已知球出手时离地面高 m,与篮圈中心的水平距离7m.当球出手后水平距离为4m时到达最大高度4m,设篮球运行的轨迹为抛物线,篮圈距地面3m.
m,与篮圈中心的水平距离7m.当球出手后水平距离为4m时到达最大高度4m,设篮球运行的轨迹为抛物线,篮圈距地面3m. 某校九年级的一场篮球比赛中,如图队员甲正在投篮,已知球出手时离地面高
某校九年级的一场篮球比赛中,如图队员甲正在投篮,已知球出手时离地面高