题目内容
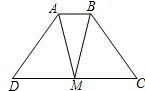已知：如图，在等腰梯形ABCD中，AD=BC，AB∥DC，M是DC的中点，求证：MA=MB．
证明：∵AD=BC，AB∥DC，
∴∠D=∠C，
∵M是DC中点，
∴DM=CM，
在△ADM和△BCM中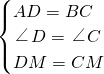
，
∴△ADM≌△BCM，
∴AM=BM．
分析：本题AD=BC，AB∥DC，得到∠D=∠C，进一步得到DM=CM，而证得由△ADM≌△BCM而解得．
点评：本题考查了等腰梯形的性质，从点的中点，到平行证得△ADM≌△BCM，从而解得．
∴∠D=∠C，
∵M是DC中点，
∴DM=CM，
在△ADM和△BCM中
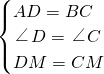，∴△ADM≌△BCM，
∴AM=BM．
分析：本题AD=BC，AB∥DC，得到∠D=∠C，进一步得到DM=CM，而证得由△ADM≌△BCM而解得．
点评：本题考查了等腰梯形的性质，从点的中点，到平行证得△ADM≌△BCM，从而解得．
练习册系列答案
名校课堂系列答案
相关题目
