题目内容
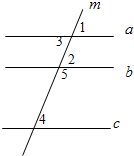 在横线上填上结论并在括号内填写相应的理由
在横线上填上结论并在括号内填写相应的理由已知:如图,∠1=∠2,∠3=∠4,则运用所学知识推理如下:
推理①∵∠1=∠2(已知)
∴
a
a
∥b
b
(同位角相等,两直线平行
同位角相等,两直线平行
)推理②又∵∠3=∠4(已知)
∴
a
a
∥c
c
(内错角相等,两直线平行
内错角相等,两直线平行
)推理③∵a∥b,a∥c(已证)
∴
b
b
∥c
c
(平行于同一条直线的两直线平行
平行于同一条直线的两直线平行
)推理④∵c∥b(已证)
∴∠4+∠5=
180°
180°
(两直线平行,同旁内角互补
两直线平行,同旁内角互补
)分析:利用平行线的判定与性质,结合图形即可得到结果.
解答:解:①∵∠1=∠2(已知)
∴a∥b(同位角相等,两直线平行)
推理②又∵∠3=∠4(已知)
∴a∥c(内错角相等,两直线平行)
推理③∵a∥b,a∥c(已证)
∴b∥c(平行于同一条直线的两直线平行)
推理④∵c∥b(已证)
∴∠4+∠5=180°(两直线平行,同旁内角互补).
故答案为:a;b;同位角相等,两直线平行;a;c;内错角相等,两直线平行;b;c;平行于同一条直线的两直线平行;180°;两直线平行,同旁内角互补
∴a∥b(同位角相等,两直线平行)
推理②又∵∠3=∠4(已知)
∴a∥c(内错角相等,两直线平行)
推理③∵a∥b,a∥c(已证)
∴b∥c(平行于同一条直线的两直线平行)
推理④∵c∥b(已证)
∴∠4+∠5=180°(两直线平行,同旁内角互补).
故答案为:a;b;同位角相等,两直线平行;a;c;内错角相等,两直线平行;b;c;平行于同一条直线的两直线平行;180°;两直线平行,同旁内角互补
点评:此题考查了平行线的判定与性质,熟练掌握平行线的判定与性质是解本题的关键.

练习册系列答案
 新卷王期末冲刺100分系列答案
新卷王期末冲刺100分系列答案 全能闯关100分系列答案
全能闯关100分系列答案
相关题目

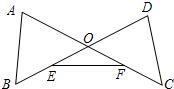 19、如图,线段AC与BD相交于点O,E、F分别为OB、OC的中点,连接AB、DC、EF分别将“∠A=∠D”记为①,“∠OEF=∠OFE”记为②,“AB=DC”记为③,要求同学从这三个等式中选出两个作为条件,一个作为结论.(在横线上填上序号)
19、如图,线段AC与BD相交于点O,E、F分别为OB、OC的中点,连接AB、DC、EF分别将“∠A=∠D”记为①,“∠OEF=∠OFE”记为②,“AB=DC”记为③,要求同学从这三个等式中选出两个作为条件,一个作为结论.(在横线上填上序号)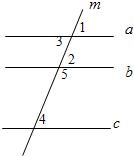 在横线上填上结论并在括号内填写相应的理由
在横线上填上结论并在括号内填写相应的理由