题目内容
如图，在矩形ABCD中，AD=2AB，点M、N分别在边AD、BC上，连接BM、DN，若四边形MBND是菱形，则
等于【 】
A．
B．
C．
D．
等于【 】A．
B． C． D．C。
∵AD=2AB，不妨设AB=1，则AD=2。
∵四边形MBND是菱形，∴MB=MD。
又∵四边形ABCD是矩形，∴∠A=90°。
设AM=x，则MB=2-x，
由勾股定理得：
，即
，解得：
。
∴MD=
。∴
。故选C。
∵四边形MBND是菱形，∴MB=MD。
又∵四边形ABCD是矩形，∴∠A=90°。
设AM=x，则MB=2-x，
由勾股定理得：
，即，解得：。∴MD=
。∴。故选C。
练习册系列答案
相关题目
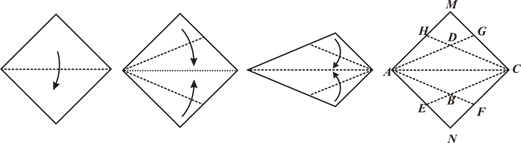
，求AB的长。
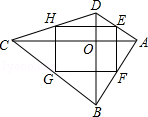
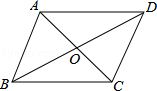
ABCD的对角线相交于点O，请你添加一个条件 （只添一个即可），使