题目内容
下列说法中:①一元二次方程都有两个根;②| 2 |
| 3 |
| 3 |
分析:对①可以举出当一元二次方程的两个根相等时,则为一个根;
对②将两个数相比与1比较即可得出谁大谁小;
对③由题可得x12+x22=7,由韦达定理可算出n的值;
对④∵(x-3)2≥0,∴b≥0.
对②将两个数相比与1比较即可得出谁大谁小;
对③由题可得x12+x22=7,由韦达定理可算出n的值;
对④∵(x-3)2≥0,∴b≥0.
解答:解:对①当方程组
无解或者两个解相等时,一元二次方程没有根或者仅有一根,所以①不正确;
对②
=
=
≥1,
∴
-
>
-2,
∴②不正确;
对③设方程x2+nx+2n=1的两个实数根为x1,x2,则x1+x2=-n,x1x2=2n-1,
又∵x12+x22=(x1+x2)2-2x1x2=n2-4n+2=7,
解得n=-1故③正确;
对④∵(x-3)2≥0,∴b≥0,故④不正确;
综上所述:答案为③.
|
对②
| ||||
|
(
| ||||||||||
(
|
| ||||
|
∴
| 2 |
| 3 |
| 3 |
∴②不正确;
对③设方程x2+nx+2n=1的两个实数根为x1,x2,则x1+x2=-n,x1x2=2n-1,
又∵x12+x22=(x1+x2)2-2x1x2=n2-4n+2=7,
解得n=-1故③正确;
对④∵(x-3)2≥0,∴b≥0,故④不正确;
综上所述:答案为③.
点评:本题考查了根与系数的关系以及估算无理数的大小,属于中等难度题型,关键掌握x1,x2是方程x2+px+q=0的两根时,x1+x2=-p,x1x2=q.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 ,则
,则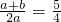 ;⑤一元二次方程x2-x=4的一次项系数是-1;⑥
;⑤一元二次方程x2-x=4的一次项系数是-1;⑥ 不是同类二次根式”中,正确的个数有_____个
不是同类二次根式”中,正确的个数有_____个 ,则
,则 ;⑤一元二次方程x2-x=4的一次项系数是-1;⑥
;⑤一元二次方程x2-x=4的一次项系数是-1;⑥ 不是同类二次根式”中,正确的个数有( )个
不是同类二次根式”中,正确的个数有( )个