ĢāÄæÄŚČŻ
”¾ĢāÄæ”æČēĶ¼£¬Ņ»“ĪŗÆŹż![]() Óė×ų±źÖį·Ö±š½»ÓŚA£¬BĮ½µć£¬Å×ĪļĻß
Óė×ų±źÖį·Ö±š½»ÓŚA£¬BĮ½µć£¬Å×ĪļĻß![]() ¾¹żµćA£¬B£¬µćP“ÓµćB³ö·¢£¬ŅŌĆæĆė2øöµ„Ī»³¤¶ČµÄĖŁ¶ČŃŲÉäĻßBAŌĖ¶Æ£¬µćQ“ÓµćA³ö·¢£¬ŅŌĆæĆė1øöµ„Ī»³¤¶ČµÄĖŁ¶ČŃŲÉäĻßAOŌĖ¶Æ£¬Į½µćĶ¬Ź±³ö·¢£¬ŌĖ¶ÆŹ±¼äĪŖtĆė£®
¾¹żµćA£¬B£¬µćP“ÓµćB³ö·¢£¬ŅŌĆæĆė2øöµ„Ī»³¤¶ČµÄĖŁ¶ČŃŲÉäĻßBAŌĖ¶Æ£¬µćQ“ÓµćA³ö·¢£¬ŅŌĆæĆė1øöµ„Ī»³¤¶ČµÄĖŁ¶ČŃŲÉäĻßAOŌĖ¶Æ£¬Į½µćĶ¬Ź±³ö·¢£¬ŌĖ¶ÆŹ±¼äĪŖtĆė£®
![]() Ēó“ĖÅ×ĪļĻߵıķ“ļŹ½£»
Ēó“ĖÅ×ĪļĻߵıķ“ļŹ½£»
![]() Ēóµ±
Ēóµ±![]() ĪŖµČŃüČż½ĒŠĪŹ±£¬ĖłÓŠĀś×ćĢõ¼žµÄtµÄÖµ£»
ĪŖµČŃüČż½ĒŠĪŹ±£¬ĖłÓŠĀś×ćĢõ¼žµÄtµÄÖµ£»
![]() µćPŌŚĻ߶ĪABÉĻŌĖ¶Æ£¬ĒėÖ±½ÓŠ“³ötĪŖŗĪÖµŹ±£¬
µćPŌŚĻ߶ĪABÉĻŌĖ¶Æ£¬ĒėÖ±½ÓŠ“³ötĪŖŗĪÖµŹ±£¬![]() µÄĆ껿“ļµ½×ī“ó£æ“ĖŹ±£¬ŌŚÅ×ĪļĻßÉĻŹĒ·ń“ęŌŚŅ»µćT£¬Ź¹µĆ
µÄĆ껿“ļµ½×ī“ó£æ“ĖŹ±£¬ŌŚÅ×ĪļĻßÉĻŹĒ·ń“ęŌŚŅ»µćT£¬Ź¹µĆ![]() ”Õ
”Õ![]() £æČō“ęŌŚ£¬ĒėÖ±½ÓŠ“³öµćTµÄ×ų±ź£»Čō²»“ęŌŚ£¬ĒėĖµĆ÷ĄķÓÉ£®
£æČō“ęŌŚ£¬ĒėÖ±½ÓŠ“³öµćTµÄ×ų±ź£»Čō²»“ęŌŚ£¬ĒėĖµĆ÷ĄķÓÉ£®

”¾“š°ø”æ(1)![]() £»£Ø2£©µ±
£»£Ø2£©µ±![]() ĪŖµČŃüČż½ĒŠĪŹ±£¬tµÄÖµĪŖ
ĪŖµČŃüČż½ĒŠĪŹ±£¬tµÄÖµĪŖ![]() ”¢
”¢![]() »ņ
»ņ![]() »ņ4£»£Ø3£©µćTµÄ×ų±źĪŖ
»ņ4£»£Ø3£©µćTµÄ×ų±źĪŖ![]() £®
£®
”¾½āĪö”æ
£Ø1£©ĻČĒóµĆµćAŗĶµćBµÄ×ų±ź£¬Č»ŗó°ŃµćAŗĶµćBµÄ×ų±źµĪ°”ČēÅ×ĪļĻߵĽāĪöŹ½æÉĒóµĆb”¢cµÄÖµ£¬“Ó¶ųæɵƵ½Å×ĪļĻߵĽāĪöŹ½£»
£Ø2£©ŌĖ¶ÆtĆėŗó£¬AQ=t£¬BP=2t£¬ĻČĒóµĆABµÄ³¤£¬Č»ŗó·ÖĪŖQA=QP£¬AP=AQ£¬PA=PQČżÖÖĒéæö£¬Ēó½ā¼“æÉ£»
£Ø3£©¹żµćP×÷PF”ĶAOÓŚµćF£¬ŃÓ³¤FP½»Å×ĪļĻßÓėµćT£®ŌņAP=4-2t£¬PF=![]() AP=2-t£¬Č»ŗóæɵƵ½S”÷APQÓėtµÄŗÆŹż¹ŲĻµŹ½£¬“Ó¶ųæÉĒóµĆtµÄÖµ£¬ÓŚŹĒæɵƵ½µćPµÄ×ų±ź£¬“Ó¶ųæÉĒóµĆµćTµÄ×ų±ź£¬Č»ŗóŌŁÖ¤Ć÷”ą”÷APT”Õ”÷APO¼“æÉ£®
AP=2-t£¬Č»ŗóæɵƵ½S”÷APQÓėtµÄŗÆŹż¹ŲĻµŹ½£¬“Ó¶ųæÉĒóµĆtµÄÖµ£¬ÓŚŹĒæɵƵ½µćPµÄ×ų±ź£¬“Ó¶ųæÉĒóµĆµćTµÄ×ų±ź£¬Č»ŗóŌŁÖ¤Ć÷”ą”÷APT”Õ”÷APO¼“æÉ£®
![]() °Ń
°Ń![]() “śČė
“śČė![]() ÖŠ£¬µĆ
ÖŠ£¬µĆ![]() £®
£®
°Ń![]() “śČė
“śČė![]() ÖŠ£¬µĆ
ÖŠ£¬µĆ![]() £®
£®
![]() £¬
£¬![]()
°Ń![]() £¬
£¬![]() ·Ö±š“śČė
·Ö±š“śČė![]() ÖŠ£¬µĆ
ÖŠ£¬µĆ![]() £¬
£¬![]() £¬
£¬
Å×ĪļĻߵıķ“ļŹ½ĪŖ![]()
![]() £¬
£¬![]() £¬Óɹ“¹É¶ØĄķ£¬µĆ
£¬Óɹ“¹É¶ØĄķ£¬µĆ![]() £¬
£¬
![]() £®
£®
ŌĖ¶ÆtĆėŗó£¬![]() £¬
£¬![]() £®
£®
![]() ĪŖµČŃüČż½ĒŠĪ£¬ÓŠ
ĪŖµČŃüČż½ĒŠĪ£¬ÓŠ![]() £¬
£¬![]() £¬
£¬![]() ČżÖÖĒéæö£¬
ČżÖÖĒéæö£¬
![]() µ±
µ±![]() Ź±£¬¹żµćQ×÷
Ź±£¬¹żµćQ×÷![]() ÓŚµćD£®
ÓŚµćD£®

ŌŚ![]() ÖŠ£¬
ÖŠ£¬![]() £¬
£¬![]()
![]() £¬
£¬
![]() £®
£®
½āµĆ![]() £»
£»
![]() µ±
µ±![]() Ź±£¬
Ź±£¬
![]() ČōµćPŌŚxÖįÉĻ·½µÄÖ±ĻßABÉĻ£¬
ČōµćPŌŚxÖįÉĻ·½µÄÖ±ĻßABÉĻ£¬![]() £¬
£¬![]() £¬
£¬
![]() £¬
£¬![]()
½āµĆ![]() £»
£»
![]() ČōµćPŌŚxÖįĻĀ·½µÄÖ±ĻßABÉĻ£¬
ČōµćPŌŚxÖįĻĀ·½µÄÖ±ĻßABÉĻ£¬
![]() £¬
£¬
![]() £¬
£¬
½āµĆ£ŗ![]() £»
£»
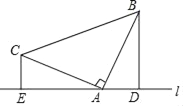
![]() µ±
µ±![]() Ź±£¬¹żµćP×÷
Ź±£¬¹żµćP×÷![]() ÓŚµćE£®
ÓŚµćE£®

Ōņ![]() £¬ŌŚ
£¬ŌŚ![]() ÖŠ£¬
ÖŠ£¬![]()
![]()
![]() £¬
£¬
![]() £®
£®
½āµĆ£ŗ![]()
×ŪÉĻĖłŹö£¬µ±![]() ĪŖµČŃüČż½ĒŠĪŹ±£¬tµÄÖµĪŖ
ĪŖµČŃüČż½ĒŠĪŹ±£¬tµÄÖµĪŖ![]() ”¢
”¢![]() »ņ
»ņ![]() »ņ4£®
»ņ4£®
![]() ¹żµćP×÷
¹żµćP×÷![]() ÓŚµćF£¬ŃÓ³¤FP½»Å×ĪļĻßÓėµćT£®
ÓŚµćF£¬ŃÓ³¤FP½»Å×ĪļĻßÓėµćT£®

![]() ĪŖ
ĪŖ![]() µ×±ßAQÉĻµÄøߣ®
µ×±ßAQÉĻµÄøߣ®
![]() £¬
£¬![]() £¬
£¬
![]() £®
£®
![]() £®
£®
![]() µ±
µ±![]() Ź±£¬
Ź±£¬![]() µÄĆ껿×ī“ó
µÄĆ껿×ī“ó![]() “ĖŹ±µćPĪŖABµÄÖŠµć£¬ĒŅ
“ĖŹ±µćPĪŖABµÄÖŠµć£¬ĒŅ![]() £®
£®
Į¬½ÓOP£¬Ōņ![]() £¬
£¬
![]() µć
µć![]() £¬
£¬
![]() µćTµÄŗį×ų±źĪŖ
µćTµÄŗį×ų±źĪŖ![]() £¬
£¬
½«![]() “śČėÅ×ĪļĻߵĽāĪöŹ½µĆ£ŗ
“śČėÅ×ĪļĻߵĽāĪöŹ½µĆ£ŗ![]() £®
£®
![]() £®
£®
ŌŚ![]() ÖŠ£¬Óɹ“¹É¶ØĄķæÉÖŖ£ŗ
ÖŠ£¬Óɹ“¹É¶ØĄķæÉÖŖ£ŗ![]() £¬
£¬
![]() £®
£®
![]() ”Õ
”Õ![]() £®
£®
![]() µćTµÄ×ų±źĪŖ
µćTµÄ×ų±źĪŖ![]() £®
£®

 ŌĶĮæģ³µĻµĮŠ“š°ø
ŌĶĮæģ³µĻµĮŠ“š°ø