题目内容
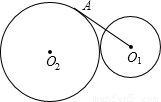
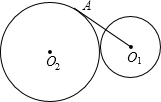如图⊙O1和⊙O2外切，它们的半径分别为1和2，过O1作⊙O2的切线，切点为A，则O1A长为分析：由于两圆外切，它们的圆心距等于两圆的半径和，连接O1O2、O2A，在构造的直角三角形中，即可根据勾股定理求得O1A的长．
解答：
解：连接O1O2，O2A；
∵⊙O1和⊙O2外切，
∴O1O2=1+2=3；
∵O1A是⊙O2的切线，
∴O2A⊥O1A，
在Rt△O1O2A中，O1O2=3，O2A=2，
由勾股定理得：O1A=
=
．
解：连接O1O2，O2A；∵⊙O1和⊙O2外切，
∴O1O2=1+2=3；
∵O1A是⊙O2的切线，
∴O2A⊥O1A，
在Rt△O1O2A中，O1O2=3，O2A=2，
由勾股定理得：O1A=
| O1O22-O2A2 |
| 5 |
点评：此题主要考查了相切两圆的性质、切线的性质以及勾股定理的综合应用，难度不大．
练习册系列答案
名校课堂系列答案
相关题目
如图⊙O1和⊙O2外切，它们的半径分别为1和2，过O1作⊙O2的切线，切点为A，则O1A长为________．
