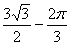题目内容
在平面直角坐标系中,抛物线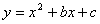 与
与 轴交于A、B两点(点A在点B的左侧),与
轴交于A、B两点(点A在点B的左侧),与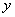 轴交于点C,点B的坐标为(3,0),将直线
轴交于点C,点B的坐标为(3,0),将直线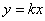 沿
沿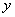 轴向上平移3个单位长度后恰好经过B、C两点。
轴向上平移3个单位长度后恰好经过B、C两点。
(1)求直线BC及抛物线的解析式;
(2)设抛物线的顶点为D,点P在抛物线的对称轴上,且 ,求点P的坐标。
,求点P的坐标。
(1) 沿
沿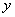 轴向上平移3个单位长度后经过
轴向上平移3个单位长度后经过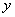 轴上的点
轴上的点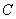 ,
, .设直线
.设直线 的解析式为
的解析式为 .
. 在直线
在直线 上,
上,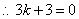 .
.
解得 ,直线
,直线 的解析式为
的解析式为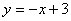 . …2分
. …2分
 抛物线
抛物线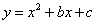 过点
过点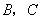 ,
,

解得
 抛物线的解析式为
抛物线的解析式为 . ……5分
. ……5分
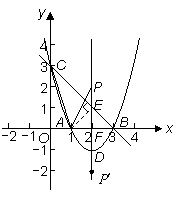 (2)由
(2)由 .
.
可得 .
.
 ,
,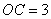 ,
, ,
, .
.
可得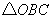 是等腰直角三角形.
是等腰直角三角形.
 ,
,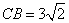 .
.
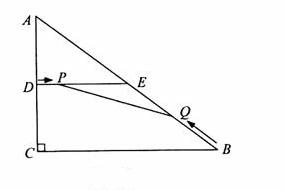
如图,设抛物线对称轴与 轴交于点
轴交于点 ,
,
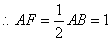 .
.
过点 作
作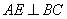 于点
于点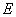 .
. .可得
.可得 ,
, .
.
在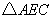 与
与 中,
中,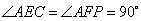 ,
,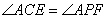 ,
,
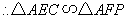 .
. ,
, .解得
.解得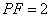 .
.
 点
点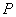 在抛物线的对称轴上,
在抛物线的对称轴上,
 点
点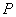 的坐标为
的坐标为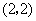 或
或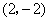

在直角梯形ABCD中,AD∥BC,∠B=∠A=90°.
操作示例
小明取直角梯形ABCD的非直角腰CD的中点P,过点P作PE∥AB,剪下△PEC(如图1),并将△PEC绕点P按逆时针方向旋转180°到△PFD的位置,拼成新的图形(如图2).
(Ⅰ)思考与实践:
(1)操作后小明发现,拼成的新图形是矩形,请帮他说明理由;
 (2)如图3四边形ABCD中AB∥CD,请你类比图2的剪拼方法,在图3画出剪拼成一个平行四边形的示意图.
(2)如图3四边形ABCD中AB∥CD,请你类比图2的剪拼方法,在图3画出剪拼成一个平行四边形的示意图.
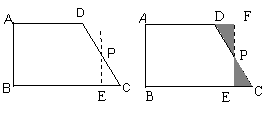 |
图1 图2
(Ⅱ)发现与运用:
|
请你选择下面两题中的一题作答:(多做不加分,两题都做按第一题计分)
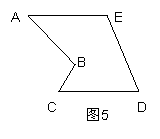
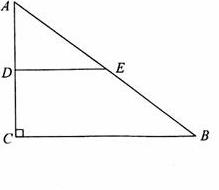
(1)如图4,在梯形ABCD中,AD∥BC,E是CD的中点, EF⊥AB于点F,AB=5,EF=4,求梯形ABCD的面积。
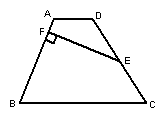
图4
(2)如图4的多边形中,AE=CD,AE∥CD,能否沿一条直线进行剪切,拼成一个平行四边形?若能,请你在图中画出剪拼的示意图并作必要的文字说明;若不能,简要说明理由.
 |
 -
- )×
)×
 、P2
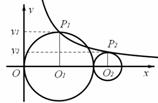
、P2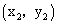 在反比例函数
在反比例函数 (x>0)的图象上,则
(x>0)的图象上,则 .
.
 ,求AB的长.
,求AB的长.
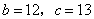 ,则sinA= .
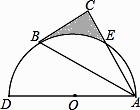
,则sinA= .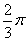 ,则图中阴影部分的面积为……( )
,则图中阴影部分的面积为……( )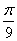 B.
B. 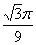 C.
C.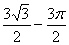 D.
D.