题目内容
抛物线y=ax2+bx+c上部分点的横坐标x,纵坐标y的对应值如下表:
从上表可知,下列说法中正确的是 .(填写序号)
①抛物线的对称轴是直线x=1; ②在对称轴右侧,y随x增大而减小;
③抛物线与x轴的一个交点为(4,0); ④函数y=ax2+bx+c的最小值为-8.
| x | … | -2 | -1 | 0 | 2 | 3 | … |
| y | … | 0 | -5 | -8 | -8 | -5 | … |
①抛物线的对称轴是直线x=1; ②在对称轴右侧,y随x增大而减小;
③抛物线与x轴的一个交点为(4,0); ④函数y=ax2+bx+c的最小值为-8.
考点:二次函数的性质
专题:探究型
分析:分别把x=0时y=-8;x=2时y=-8及x=-1时y=-5代入抛物线y=ax2+bx+c求出函数的解析式,再根据二次函数的性质进行解答即可.
解答:解:∵x=0时y=-8;x=2时y=-8及x=-1时y=-5,
∴
,解得
,
∴此抛物线的解析式为:y=x2-2x-8,即y=(x-1)2-9,
∴此抛物线的对称轴是x=1,故①正确;
∵a=1>0,
∴此抛物线开口向上,y随x增大而增大,故②错误;
∵当x=4时,y=0,
∴抛物线与x轴的一个交点为(4,0),故③正确;
∵抛物线的顶点坐标为(1,-9),
∴函数y=ax2+bx+c的最小值为-9,故④错误.
故答案为:①③.
∴
|
|
∴此抛物线的解析式为:y=x2-2x-8,即y=(x-1)2-9,
∴此抛物线的对称轴是x=1,故①正确;
∵a=1>0,
∴此抛物线开口向上,y随x增大而增大,故②错误;
∵当x=4时,y=0,
∴抛物线与x轴的一个交点为(4,0),故③正确;
∵抛物线的顶点坐标为(1,-9),
∴函数y=ax2+bx+c的最小值为-9,故④错误.
故答案为:①③.
点评:本题考查的是二次函数的性质及用待定系数法求二次函数的解析式,先根据题意求出a、b、c的值是解答此题的关键.

练习册系列答案
 科学实验活动册系列答案
科学实验活动册系列答案
相关题目
在实数0、-
、|-3|、-
中,最小的是( )
| 2 |
| 2 |
| 3 |
| A、0 | ||
B、-
| ||
| C、|-3| | ||
D、-
|
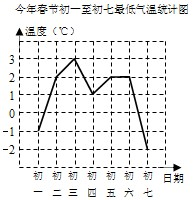 小华同学根据某地今年春节初一至初七的每天最低气温绘成了所示的折线统计图.关于这7天的每天最低气温的说法不正确的是( )
小华同学根据某地今年春节初一至初七的每天最低气温绘成了所示的折线统计图.关于这7天的每天最低气温的说法不正确的是( )| A、极差是5℃ |
| B、众数是2℃ |
| C、中位数是1℃ |
| D、平均数是1℃ |
 如图,AD是△ABC的中线,E是AD上的一点,且AE=
如图,AD是△ABC的中线,E是AD上的一点,且AE=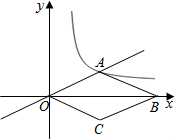 如图,正比例函数
如图,正比例函数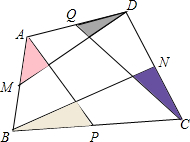 如图,在四边形ABCD中,M为AB的中点,P为BC的中点,N为CD的中点,Q为DA的中点,若图中中间的小四边形的面积为1,试求四个小三角形(阴影部分)面积之和.
如图,在四边形ABCD中,M为AB的中点,P为BC的中点,N为CD的中点,Q为DA的中点,若图中中间的小四边形的面积为1,试求四个小三角形(阴影部分)面积之和.