题目内容
已知实数a,b,x,y满足ax+by=3,ay-bx=5,求(a2+b2)(x2+y2).
分析:先把已知式子平方,再相加,把求的代数式展开,即可得出答案.
解答:解:∵ax+by=3,ay-bx=5,
∴两边平方得:(ax+by)2=9,(ay-bx)2=25,
a2x2+2abxy+b2y2=9,a2y2-2abxy+b2x2=25,
相加得:a2x2+by2+a2y2+b2x2=34,
∴(a2+b2)(x2+y2)=a2x2+by2+a2y2+b2x2=34.
∴两边平方得:(ax+by)2=9,(ay-bx)2=25,
a2x2+2abxy+b2y2=9,a2y2-2abxy+b2x2=25,
相加得:a2x2+by2+a2y2+b2x2=34,
∴(a2+b2)(x2+y2)=a2x2+by2+a2y2+b2x2=34.
点评:本题考查了完全平方公式,整式的混合运算的应用,主要考查学生的化简能力和计算能力.

练习册系列答案
相关题目
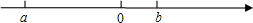 已知实数a、b在数轴上的位置如图.
已知实数a、b在数轴上的位置如图.