题目内容
 如图,在方格纸中,∠ABC=∠1,∠BCD=∠2,∠CDE=∠3,则∠1,∠2,∠3的大小关系是
如图,在方格纸中,∠ABC=∠1,∠BCD=∠2,∠CDE=∠3,则∠1,∠2,∠3的大小关系是
- A.∠1<∠2<∠3
- B.∠1=∠2>∠3
- C.∠1=∠2=∠3
- D.∠1>∠2>∠3
B
分析:根据平行线的性质和全等的知识可得3个角的大小关系.
解答: 解:易得△ABF≌△DCG,
解:易得△ABF≌△DCG,
∴∠ABF=∠DCG,
∵BF∥CG∥HD,
∴∠FBC=∠BCG,∠GCD=∠CDH,
∴∠1=∠ABC=∠ABF+∠FBC,∠2=∠BCD=∠DCG+∠BCG,
∴∠1=∠2,
∵tan∠HDE= =
= ,tan∠GCB=
,tan∠GCB= ,
,
∴∠GCB>∠HDE,
∵∠3=∠CDH=∠CDH+∠HDE<∠DCG+∠BCG=∠2,
∴∠1=∠2>∠3.
故选B.
点评:综合考查了全等三角形的判定与性质及平行线的性质;得到相关角的等量关系是解决本题的关键.
分析:根据平行线的性质和全等的知识可得3个角的大小关系.
解答:
 解:易得△ABF≌△DCG,
解:易得△ABF≌△DCG,∴∠ABF=∠DCG,
∵BF∥CG∥HD,
∴∠FBC=∠BCG,∠GCD=∠CDH,
∴∠1=∠ABC=∠ABF+∠FBC,∠2=∠BCD=∠DCG+∠BCG,
∴∠1=∠2,
∵tan∠HDE=
 =
= ,tan∠GCB=
,tan∠GCB= ,
,∴∠GCB>∠HDE,
∵∠3=∠CDH=∠CDH+∠HDE<∠DCG+∠BCG=∠2,
∴∠1=∠2>∠3.
故选B.
点评:综合考查了全等三角形的判定与性质及平行线的性质;得到相关角的等量关系是解决本题的关键.

练习册系列答案
相关题目
 9、如图,在方格纸中,有一平行四边形ABCD,则它关于x轴对称图形的顶点坐标是(2,-1)、(4,-1)、(6,-3)和( )
9、如图,在方格纸中,有一平行四边形ABCD,则它关于x轴对称图形的顶点坐标是(2,-1)、(4,-1)、(6,-3)和( )
 (2013•百色)如图,在方格纸中,每个小方格都是边长为1cm的正方形,△ABC的三个顶点都在格点上,将△ABC绕点O逆时针旋转90°后得到△A′B′C′(其中A、B、C的对应点分别为A′,B′,C′,则点B在旋转过程中所经过的路线的长是
(2013•百色)如图,在方格纸中,每个小方格都是边长为1cm的正方形,△ABC的三个顶点都在格点上,将△ABC绕点O逆时针旋转90°后得到△A′B′C′(其中A、B、C的对应点分别为A′,B′,C′,则点B在旋转过程中所经过的路线的长是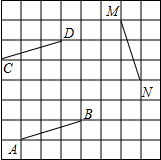 如图,在方格纸中给出了线段AB、CD、MN.根据你所学的知识和方法,写出它们之间的位置关系.
如图,在方格纸中给出了线段AB、CD、MN.根据你所学的知识和方法,写出它们之间的位置关系. 如图,在方格纸中,直线m与n相交于点C,
如图,在方格纸中,直线m与n相交于点C,