题目内容
如图,关于x的二次函数y=x2-2mx-m-2的图象与x轴交于A(x1,0)、B(x2,0)两点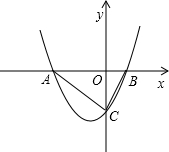 (x1<0<x2),与y轴交于C点
(x1<0<x2),与y轴交于C点
(1)当m为何值时,AC=BC;
(2)当∠BAC=∠BCO时,求这个二次函数的表达式.
 (x1<0<x2),与y轴交于C点
(x1<0<x2),与y轴交于C点(1)当m为何值时,AC=BC;
(2)当∠BAC=∠BCO时,求这个二次函数的表达式.
(1)要使AC=BC,则该抛物线的对称轴应是y轴,
则有-
=0,即m=0,
∴当m=0时,AC=BC.
(2)当∠BAC=∠BCO,有Rt△AOC∽Rt△COB,则
=
,
即OC2=OA•OB,
由题意,知OC=|-m-2|,OA=|x1|=-x1,OB=|x2|=x2
由根与系数关系,得x1x2=-m-2,
∴OA•OB=-x1x2=m+2
则|-m-2|2=m+2,
解,得m=-2或m=-1.
当m=-2时,二次函数为y=x2+4x,此时x1=-4,x2=0,不合题意,舍去.
当m=-1时,二次函数为y=x2+2x-1,此时x1=-1-
,x2=-1+
,符合题意.
∴当∠BAC=∠BCO时,这个二次函数的表达式为y=x2+2x-1.
则有-
| -2m |
| 2×1 |
∴当m=0时,AC=BC.
(2)当∠BAC=∠BCO,有Rt△AOC∽Rt△COB,则
| OC |
| OB |
| OA |
| OC |
即OC2=OA•OB,
由题意,知OC=|-m-2|,OA=|x1|=-x1,OB=|x2|=x2
由根与系数关系,得x1x2=-m-2,
∴OA•OB=-x1x2=m+2
则|-m-2|2=m+2,
解,得m=-2或m=-1.
当m=-2时,二次函数为y=x2+4x,此时x1=-4,x2=0,不合题意,舍去.
当m=-1时,二次函数为y=x2+2x-1,此时x1=-1-
| 2 |
| 2 |
∴当∠BAC=∠BCO时,这个二次函数的表达式为y=x2+2x-1.

练习册系列答案
相关题目
 抛物线对称轴为直线x=-3.
抛物线对称轴为直线x=-3.
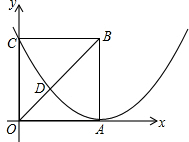
 的厚度)
的厚度)