题目内容
已知1+x+x2+…+x2004+x2005=0，则x2006= ．
考点：因式分解的应用
专题：
分析：在1+x+x2+…+x2004+x2005中加上x2006后提公因式即可求得答案．
解答：解：∵1+x+x2+…+x2004+x2005=0，
∴x2006+1+x+x2+…+x2004+x2005=1+x（1+x+x2+…+x2004+x2005）=1，
∴x2006=1．
故答案为：1．
∴x2006+1+x+x2+…+x2004+x2005=1+x（1+x+x2+…+x2004+x2005）=1，
∴x2006=1．
故答案为：1．
点评：此题考查了因式分解的应用；解题的关键是根据已知条件对要求的式子进行因式分解．
练习册系列答案
相关题目
将点P（2，-3）绕原点旋转180度得到的点的坐标为（ ）
| A、（-2，-3） |
| B、（2，-3） |
| C、（-2，3） |
| D、（2，3） |
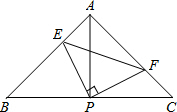如图，已知△ABC中，AB=AC，∠BAC=90°，直角∠EPF的顶点P是BC中点，两边PE、PF分别交AB、AC于点E、F，给出以下四个结论：①AE=CF； ②△EPF是等腰直角三角形； ③S四边形AEPF=