题目内容
如图,等腰梯形花圃ABCD的底边AD靠墙,另三边用长为40米的铁栏杆围成,设该花圃的腰AB的长为x米.
(1)请求出底边BC的长(用含x的代数式表示);
(2)若∠BAD=60°, 该花圃的![]() 面积为S米2.
面积为S米2.
①求S与x之间的函数关系式(要指出自变量x的取值范围),并求当S=![]() 时x的值;
时x的值;
②如果墙长为24米,试问S有最大值还是最小值?这个值是多少?

解:(1)∵AB=CD=x米,∴BC=40-AB-CD=(40-2x)米.
 (2)①如图,过点B、C分别作BE⊥AD于E,CF⊥AD于F,在Rt△ABE中,AB=x,∠BAE=60°
(2)①如图,过点B、C分别作BE⊥AD于E,CF⊥AD于F,在Rt△ABE中,AB=x,∠BAE=60°
∴AE=![]() x,BE=
x,BE=![]() x.同理DF=
x.同理DF=![]() x,CF=
x,CF=![]() x
x
又EF=BC=40-2x
∴AD=AE+EF+DF=![]() x+40-2x+
x+40-2x+![]() x=40-x
x=40-x
 ∴S=
∴S=![]() (40-2x+40-x)·
(40-2x+40-x)·![]() x=
x=![]() x(80-3x)
x(80-3x)
=![]() (0<x<20)
(0<x<20)
当S=![]() 时,
时,![]() =
=![]()
解得:x1=6,x2=![]() (舍去).∴x=
(舍去).∴x=![]() 6…
6…
②由题意,得40-x≤24,解得x≥16,
结合①得16![]() ≤x<20
≤x<20
由①,S=![]() =
=![]()
∵a=![]() <0
<0
∴函数图象为开口向下的抛物线的一段(附函数图象草图如左).
其对称轴为x=![]() ,∵16>
,∵16>![]() ,由左图可知,
,由左图可知,
当16≤x<20时,S随x的增大而减小……………………………(11分)
∴当x=16时,S取得最大值,………………………………………(12分)
此时S最大值=![]() .…………………(13分)
.…………………(13分)

练习册系列答案
相关题目
 腰AB的长为x米.
腰AB的长为x米. 时x的值;
时x的值;
 时x的值;
时x的值;
 时x的值;
时x的值;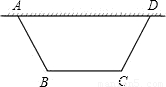
 时x的值;
时x的值;