题目内容
15.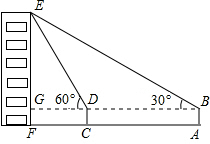 如图,小俊在A处利用高为1.5米的测角仪AB测得楼EF顶部E的仰角为30°,然后前进12米到达C处,又测得楼顶E的仰角为60°,求楼EF的高度.(结果精确到0.1米)
如图,小俊在A处利用高为1.5米的测角仪AB测得楼EF顶部E的仰角为30°,然后前进12米到达C处,又测得楼顶E的仰角为60°,求楼EF的高度.(结果精确到0.1米)
分析 设楼EF的高为x米,由EG=EF-GF表示出EG,根据题意得到EF与AF垂直,DC与AF垂直,BA与AF垂直,BD与EF垂直,在直角三角形EGD中,利用锐角三角函数定义表示出DG,在直角三角形EGB中,利用锐角三角函数定义表示出BG,根据BG-DG表示出DB,即为CA,根据CA的长列出关于x的方程,求出方程的解即可得到结果.
解答 解:设楼EF的高为x米,可得EG=EF-GF=(x-1.5)米,
依题意得:EF⊥AF,DC⊥AF,BA⊥AF,BD⊥EF(设垂足为G),
在Rt△EGD中,DG=$\frac{EG}{tan∠EDG}$=$\frac{\sqrt{3}}{3}$(x-1.5)米,在Rt△EGB中,BG=$\sqrt{3}$(x-1.5)米,
∴CA=DB=BG-DG=$\frac{2\sqrt{3}}{3}$(x-1.5)米,
∵CA=12米,∴$\frac{2\sqrt{3}}{3}$(x-1.5)=12,
解得:x=6$\sqrt{3}$+1.5≈11.9,
则楼EF的高度约为11.9米.
点评 此题考查了解直角三角形的应用-仰角俯角问题,要求学生能借助仰角构造直角三角形并解直角三角形.

练习册系列答案
 数学奥赛暑假天天练南京大学出版社系列答案
数学奥赛暑假天天练南京大学出版社系列答案 南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
相关题目
5.方程x2-2x+3=0的根的情况是( )
| A. | 有两个相等的实数根 | B. | 只有一个实数根 | ||
| C. | 没有实数根 | D. | 有两个不相等的实数根 |
8.下列说法正确的是( )
| A. | 随机抛一枚硬币,落地后正面一定朝上 | |
| B. | 调查重庆市民对诺贝尔文学奖获得者莫言的知晓情况用普查 | |
| C. | 在一副没有大小王的扑克牌中任意抽一张,抽到的牌是6的概率是$\frac{1}{13}$ | |
| D. | 在一次抽奖活动中,”中奖率是$\frac{1}{100}$”表示抽奖100次就一定会中奖 |
 如图,已知直线m∥n,∠1=100°,则∠2的度数为80°.
如图,已知直线m∥n,∠1=100°,则∠2的度数为80°.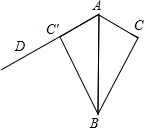 如图,△ABC的面积等于6,边AC=3,现将△ABC沿AB所在直线翻折,使点C落在直线AD上的C′处,点P在直线AD上,则线段BP的长不可能是( )
如图,△ABC的面积等于6,边AC=3,现将△ABC沿AB所在直线翻折,使点C落在直线AD上的C′处,点P在直线AD上,则线段BP的长不可能是( )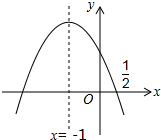 如图,抛物线y=ax2+bx+c的对称轴是x=-1.且过点($\frac{1}{2}$,0),有下列结论:①abc>0;②a-2b+4c=0;③25a-10b+4c=0;④3b+2c>0;⑤a-b≥m(am-b);其中所有正确的结论是①③⑤.(填写正确结论的序号)
如图,抛物线y=ax2+bx+c的对称轴是x=-1.且过点($\frac{1}{2}$,0),有下列结论:①abc>0;②a-2b+4c=0;③25a-10b+4c=0;④3b+2c>0;⑤a-b≥m(am-b);其中所有正确的结论是①③⑤.(填写正确结论的序号)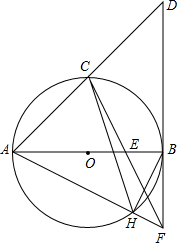 如图,AB是⊙的直径,C是$\widehat{AB}$的中点,BD⊥AB交AC的延长线于点D,E是OB的中点,CE的延长线交DB于F,AF交⊙O于H,连接BH.
如图,AB是⊙的直径,C是$\widehat{AB}$的中点,BD⊥AB交AC的延长线于点D,E是OB的中点,CE的延长线交DB于F,AF交⊙O于H,连接BH. 如图,把长方形纸片ABCD沿EF对折,若∠1=40°,则∠AEF=110°.
如图,把长方形纸片ABCD沿EF对折,若∠1=40°,则∠AEF=110°.