题目内容
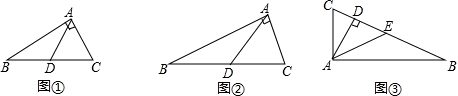
在△ABC中,AB=AC=20,BC=32,点D在BC上,且AD=13,求BD的长.
【考点】勾股定理.
【分析】过点A作AE⊥BC于E,根据等腰三角形三线合一的性质可得BE=CE= BC,再利用勾股定理列式求出AE,然后利用勾股定理列式求出DE,即可得解.
BC,再利用勾股定理列式求出AE,然后利用勾股定理列式求出DE,即可得解.
【解答】解:如图,过点A作AE⊥BC于E,
∵AB=AC,
∴BE=CE= BC=16,
BC=16,
由勾股定理得,AE= =
= =12,
=12,
在Rt△ADE中,DE= =
= =5,
=5,
当点D在AE左侧时(如图)BD=BE﹣DE=16﹣5=11;
当点D在AE右侧时,BD=BE+DE=16+5=21.
综上所述,BD的长为11或21.

【点评】本题考查的是勾股定理,根据题意作辅助线构造出直角三角形是解题的关键.

练习册系列答案
相关题目
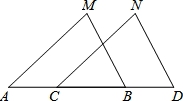


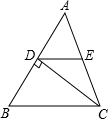

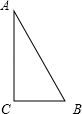
 ,连结BE,再证△ABC≌△BAE,你认为小聪能否完成证明?__________(只需要填“能”或“不能”);
,连结BE,再证△ABC≌△BAE,你认为小聪能否完成证明?__________(只需要填“能”或“不能”);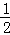 BC,请你帮助小聪同学
BC,请你帮助小聪同学 完成;
完成;