��Ŀ����
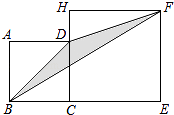
����Ŀ����ͼ�٣�OABC��һ�ŷ���ƽ��ֱ������ϵ�еľ���ֽƬ��OΪԭ�㣬��A��x����������ϣ���C��y����������ϣ�OA=5��OC=4��
��1����OC����ȡһ��D����ֽƬ��AD���ۣ�ʹ��O����BC���ϵĵ�E������D���������E������� ��
��2����ͼ�ڣ���AE����һ����P������A��E�غϣ���A����AE������E�������˶����˶����ٶ�Ϊÿ��1����λ���ȣ����˶���ʱ��Ϊt�루0��t��5������P����ED��ƽ���߽�AD�ڵ�M������M��AE��ƽ���߽�DE�ڵ�N�����ı���PMNE�����S��ʱ��t֮��ĺ�����ϵʽ��tȡ��ֵʱ��S�����ֵ�����ֵ�Ƕ��٣�
��3���ڣ�2���������£���tΪ��ֵʱ����A��M��EΪ�����������Ϊ���������Σ��������Ӧʱ�̵�M�����꣮
���𰸡�
��1����0,2.5��,��2,4��
��2���⣺��PM��ED��
���APM�ס�AED��
��PM��ED=AP��AE��
��PM= ![]() ��
��
�֡�AP=t��ED=2.5��AE=5��
��PM= ![]() =
= ![]() t��
t��
��PM��DE��MN��EP��
���ı���NMPEΪƽ���ı��Σ�
�֡ߡ�DEA=90�㣬
���ı���PMNEΪ���Σ�
��S����PMNE=PMPE= ![]() t��5��t��=��
t��5��t��=�� ![]() t2+
t2+ ![]() t��
t��
��S����PMNE=�� ![]() ��t��
��t�� ![]() ��2+
��2+ ![]() ��
��
�֡�0�� ![]() ��5��
��5��
�൱t= ![]() ʱ��S����PMNE�����ֵ
ʱ��S����PMNE�����ֵ ![]() ��
��
��3���⣺��������AEΪ���������εĵף���ME=MA����ͼ�٣�
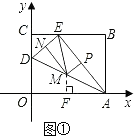
��Rt��AED��ME=MA��
��PM��AE��
��PΪAE���е㣬
��t=AP= ![]() AE=2.5��
AE=2.5��
�֡�PM��ED��
��MΪAD���е㣮
����M��MF��OA������ΪF����MF�ǡ�OAD����λ�ߣ�
��MF= ![]() OD=
OD= ![]() ��OF=
��OF= ![]() OA=2.5��
OA=2.5��
�൱t=2.5ʱ����0��2.5��5������AMEΪ���������Σ�
��ʱM������Ϊ��2.5��1.25����
��������AEΪ���������ε�������AM=AE=5����ͼ�ڣ�
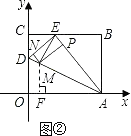
��Rt��AOD��AD= ![]() =
= ![]() ��
��
����M��MF��OA������ΪF��
��PM��ED��
���APM�ס�AED��
��AP��AE=AM��AD��
��t=AP= ![]() =2
=2 ![]() ��
��
��PM= ![]() t=
t= ![]() ��
��
��MF=MP= ![]() ��OF=OA��AF=OA��AP=5��2
��OF=OA��AF=OA��AP=5��2 ![]() ��
��
�൱t=2 ![]() ʱ����0��2
ʱ����0��2 ![]() ��5������ʱM������Ϊ��5��2
��5������ʱM������Ϊ��5��2 ![]() ��
�� ![]() ����
����
������ͼ�ο�֪EM=EA�������������
�ۺ�������������t=2.5��t=2 ![]() ʱ����A��M��EΪ�����������Ϊ���������Σ���ӦM�������Ϊ��
ʱ����A��M��EΪ�����������Ϊ���������Σ���ӦM�������Ϊ�� ![]() ��
�� ![]() ����5��2
����5��2 ![]() ��
�� ![]() ����
����
���������⣺��1���������֪���ۺ�AD���ı���OAED�ĶԳ��ᣬ
����Rt��ABE��AE=AO=5��AB=4��BE= ![]() =3��
=3��
��CE=2��
��E��������2��4����
��Rt��DCE��DC2+CE2=DE2��
�֡�DE=OD��
�ࣨ4��OD��2+22=OD2��
��ã�OD=2.5��
��D��������0��2.5����
���Դ��ǣ���0��2.5������2��4����
�����㾫����������Ҫ�����˶��κ�������ֵ���ɶ����ĸ�������֪ʶ�㣬��Ҫ��������Ա�����ȡֵ��Χ��ȫ��ʵ������ô�����ڶ��㴦ȡ�����ֵ������Сֵ��������x=-b/2aʱ��y��ֵ=(4ac-b2)/4a��ֱ����������ֱ�DZ�a��b��ƽ���͵���б��c��ƽ��,��;a2+b2=c2������ȷ�����⣮