题目内容
如图所示,已知直线y=kx+m与x轴、y轴分别交于A、C两点,抛物线y=-x2+bx+c经过A、C两点,点B是抛物线与x轴的另一个交点,当![]() 时,y取最大值
时,y取最大值![]() .
.

(1)求抛物线和直线的解析式;
(2)设点P是直线AC上一点,且S△ABP:S△BPC=1∶3,求点P的坐标;
(3)若直线![]() 与(1)中所求的抛物线交于M、N两点,问:
与(1)中所求的抛物线交于M、N两点,问:
①是否存在a的值,使得∠MON=90°?若存在,求出a的值;若不存在,请说明理由;
②猜想当∠MON>90°时,a的取值范围(不写过程,直接写结论).
(参考公式:在平面直角坐标系中,若M(x1,y1),N(x2,y2),则M,N两点间的距离为![]() )
)
答案:
解析:
解析:
|
解:(1)由题意得 解得 ∴抛物线的解析式为 ∴ ∴直线 (2)分两种情况: ①点 ∵ ∴ ∵ ∴ ∴ ∴ ∴ ②点 ∵ ∴ ∵ ∴ ∴ ∴ ∴ 综上所述, (3)①方法1:假设存在 由 得 ∴ 又 ∴ ∵ ∴ ∴ ∴ ∴ 即 ∴ ∴存在 方法2:假设存在 可证明 ∴ 即 ∴ 即 以下过程同上 ②当 |

练习册系列答案
相关题目


 三角形?若存在,求出点C的坐标,并证明;若不存在,请说明理由.
三角形?若存在,求出点C的坐标,并证明;若不存在,请说明理由. 4、如图所示,已知直线a∥b,被直线L所截,如果∠1=69°36′,那么∠2=
4、如图所示,已知直线a∥b,被直线L所截,如果∠1=69°36′,那么∠2= 平移,设平移过程中△F′O′G′与四边形ODCE重叠部分面积为y,OO′的长为x(0≤x≤1),求y与x的函数关系式.
平移,设平移过程中△F′O′G′与四边形ODCE重叠部分面积为y,OO′的长为x(0≤x≤1),求y与x的函数关系式.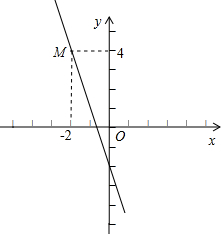 如图所示,已知直线y=kx-2经过M点,求此直线与x轴交点坐标和直线与两坐标轴围成三角形的面积.
如图所示,已知直线y=kx-2经过M点,求此直线与x轴交点坐标和直线与两坐标轴围成三角形的面积. 如图所示:已知直线y=
如图所示:已知直线y=