题目内容
如图,已知直线l1:y= x+
x+ 与直线l2:y=-2x+16相交于点C,l1、l2分别交x轴于A、B两点.矩形DEFG的顶点D、E分别在直线l1、l2上,顶点F、G都在x轴上,且点G与点B重合.
与直线l2:y=-2x+16相交于点C,l1、l2分别交x轴于A、B两点.矩形DEFG的顶点D、E分别在直线l1、l2上,顶点F、G都在x轴上,且点G与点B重合.(1)求△ABC的面积;
(2)求矩形DEFG的边DE与EF的长;
(3)若矩形DEFG沿x轴的反方向以每秒1个单位长度的速度平移,设移动时间为t(0≤t≤12)秒,矩形DEFG与△ABC重叠部分的面积为S,求S关于t的函数关系式,并写出相应的t的取值范围.

【答案】分析:(1)把y=0代入l1解析式求出x的值便可求出点A的坐标.令x=0代入l2的解析式求出点B的坐标.然后可求出AB的长.
联立方程组可求出交点C的坐标,继而求出三角形ABC的面积.
(2)已知xD=xB=8易求D点坐标.又已知yE=yD=8可求出E点坐标.故可求出DE,EF的长.
(3)作CM⊥AB于M,证明Rt△RGB∽Rt△CMB利用线段比求出RG=2t.又知道S=S△ABC-S△BRG-S△AFH,根据三角形面积公式可求出S关于t的函数关系式.
解答:解:(1)由 x+
x+ =0,得x=-4.
=0,得x=-4.
∴A点坐标为(-4,0),
由-2x+16=0,
得x=8.
∴B点坐标为(8,0),
∴AB=8-(-4)=12,
由 ,解得
,解得
∴C点的坐标为(5,6),
∴S△ABC= AB•yC=
AB•yC= ×12×6=36.
×12×6=36.
(2)∵点D在l1上且xD=xB=8,
∴yD= ×8+
×8+ =8,
=8,
∴D点坐标为(8,8),
又∵点E在l2上且yE=yD=8,
∴-2xE+16=8,
∴xE=4,
∴E点坐标为(4,8),
∴DE=8-4=4,EF=8.
(3)①当0≤t<3时,如图1,矩形DEFG与△ABC重叠部分为五边形CHFGR(t=0时,为四边形CHFG).
过C作CM⊥AB于M,则Rt△RGB∽Rt△CMB,
∴ ,即
,即 ,∴RG=2t,
,∴RG=2t,
∵Rt△AFH∽Rt△AMC,
∴S=S△ABC-S△BRG-S△AFH=36- ×t×2t-
×t×2t- (8-t)×
(8-t)× (8-t),
(8-t),
即S=- t2+
t2+ t+
t+ .
.
②当3≤t<8时,如图2所示,矩形DEFG与△ABC重叠部分为梯形HFGR,由①知,HF= (8-t),
(8-t),
∵Rt△AGR∽Rt△AMC,
∴ =
= ,即
,即 =
= ,∴RG=
,∴RG= (12-t),
(12-t),
∴S= (HF+RG)×FG=
(HF+RG)×FG= [
[ (8-t)+
(8-t)+ (12-t)]×4,
(12-t)]×4,
即S=- t+
t+ ;
;
③当8≤t≤12时,如图3所示,矩形DEFG与△ABC重叠部分为△AGR,
由②知,AG=12-t,RG= (12-t),
(12-t),
∴S= AG•RG=
AG•RG= (12-t)×
(12-t)× (12-t)即S=
(12-t)即S= (12-t)2,
(12-t)2,
∴S= t2-8t+48.
t2-8t+48.
点评:本题属于大综合题目,主要考查的知识点有一次函数、二次函数、方程组与平移、三角形的面积、三角形的相似等知识点.解决本题的关键是理顺各知识点间的关系,还要善于分解,化整为零,各个击破.
联立方程组可求出交点C的坐标,继而求出三角形ABC的面积.
(2)已知xD=xB=8易求D点坐标.又已知yE=yD=8可求出E点坐标.故可求出DE,EF的长.
(3)作CM⊥AB于M,证明Rt△RGB∽Rt△CMB利用线段比求出RG=2t.又知道S=S△ABC-S△BRG-S△AFH,根据三角形面积公式可求出S关于t的函数关系式.
解答:解:(1)由
 x+
x+ =0,得x=-4.
=0,得x=-4.∴A点坐标为(-4,0),
由-2x+16=0,
得x=8.
∴B点坐标为(8,0),
∴AB=8-(-4)=12,
由
 ,解得
,解得
∴C点的坐标为(5,6),
∴S△ABC=
 AB•yC=
AB•yC= ×12×6=36.
×12×6=36.(2)∵点D在l1上且xD=xB=8,
∴yD=
 ×8+
×8+ =8,
=8,∴D点坐标为(8,8),
又∵点E在l2上且yE=yD=8,
∴-2xE+16=8,
∴xE=4,
∴E点坐标为(4,8),
∴DE=8-4=4,EF=8.
(3)①当0≤t<3时,如图1,矩形DEFG与△ABC重叠部分为五边形CHFGR(t=0时,为四边形CHFG).
过C作CM⊥AB于M,则Rt△RGB∽Rt△CMB,
∴
 ,即
,即 ,∴RG=2t,
,∴RG=2t,∵Rt△AFH∽Rt△AMC,
∴S=S△ABC-S△BRG-S△AFH=36-
 ×t×2t-
×t×2t- (8-t)×
(8-t)× (8-t),
(8-t),
即S=-
 t2+
t2+ t+
t+ .
.②当3≤t<8时,如图2所示,矩形DEFG与△ABC重叠部分为梯形HFGR,由①知,HF=
 (8-t),
(8-t),∵Rt△AGR∽Rt△AMC,
∴
 =
= ,即
,即 =
= ,∴RG=
,∴RG= (12-t),
(12-t),∴S=
 (HF+RG)×FG=
(HF+RG)×FG= [
[ (8-t)+
(8-t)+ (12-t)]×4,
(12-t)]×4,即S=-
 t+
t+ ;
;③当8≤t≤12时,如图3所示,矩形DEFG与△ABC重叠部分为△AGR,
由②知,AG=12-t,RG=
 (12-t),
(12-t),∴S=
 AG•RG=
AG•RG= (12-t)×
(12-t)× (12-t)即S=
(12-t)即S= (12-t)2,
(12-t)2,∴S=
 t2-8t+48.
t2-8t+48.点评:本题属于大综合题目,主要考查的知识点有一次函数、二次函数、方程组与平移、三角形的面积、三角形的相似等知识点.解决本题的关键是理顺各知识点间的关系,还要善于分解,化整为零,各个击破.

练习册系列答案
 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案
相关题目
 6、如图,已知直线l1,l2,l3相交于点O,∠1=35°,∠2=25°,则∠3等于( )
6、如图,已知直线l1,l2,l3相交于点O,∠1=35°,∠2=25°,则∠3等于( ) (2012•郯城县一模)如图,已知直线l1∥l2∥l3∥l4,相邻两条平行直线间的距离都是1,如果正方形ABCD的四个顶点分别在四条直线上,则cosα=( )
(2012•郯城县一模)如图,已知直线l1∥l2∥l3∥l4,相邻两条平行直线间的距离都是1,如果正方形ABCD的四个顶点分别在四条直线上,则cosα=( )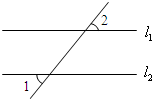 (2007•黔南州)如图,已知直线l1∥l2,∠1=50°,那么∠2=
(2007•黔南州)如图,已知直线l1∥l2,∠1=50°,那么∠2= 如图:已知直线l1∥l2,且l3、l4和l1、l2分别交于点A、B和点C、D,点P在AB上,设∠ADP=∠1,∠DPC=∠2,∠BCP=∠3.
如图:已知直线l1∥l2,且l3、l4和l1、l2分别交于点A、B和点C、D,点P在AB上,设∠ADP=∠1,∠DPC=∠2,∠BCP=∠3.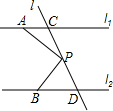 如图,已知直线l1∥l2,直线l3和直线l1、l2交于点C和D,在直线l3上有点P(点P与点C、D不重合),点A在直线l1上,点B在直线l2上.
如图,已知直线l1∥l2,直线l3和直线l1、l2交于点C和D,在直线l3上有点P(点P与点C、D不重合),点A在直线l1上,点B在直线l2上.