题目内容
某数学兴趣小组,利用树影测量树高.已测出树AB的影长AC为9米,并测出此时太阳光线与地面成30°夹角.(1)求出树高AB;
(2)因水土流失,此时树AB沿太阳光线方向倒下,在倾倒过程中,树影长度发生了变化,假设太阳光线与地面夹角保持不变,试求树
 影的最大长度.(计算结果精确到0.1米,参考数据:
影的最大长度.(计算结果精确到0.1米,参考数据:| 2 |
| 3 |
分析:(1)可根据正切值求出树高AB;
(2)以点A为圆心,以AB为半径作圆弧,当太阳光线与圆弧相切时树影最长,点D为切点,DE⊥AD交AC于E点,求出AE的值即可.
(2)以点A为圆心,以AB为半径作圆弧,当太阳光线与圆弧相切时树影最长,点D为切点,DE⊥AD交AC于E点,求出AE的值即可.
解答: 解:(1)在Rt△ABC中,∠BAC=90°,∠C=30°
解:(1)在Rt△ABC中,∠BAC=90°,∠C=30°
∵tanC=
(2分)
∴AB=AC•tanC(3分)
=9×
(4分)
≈5.2(米)(5分)
(2)以点A为圆心,以AB为半径作圆弧,当太阳光线与圆弧相切时树影最长,点D为切点,DE⊥AD交AC于E点,(如图)(7分)
在Rt△ADE中,∠ADE=90°,∠E=30°,
∴AE=2AD(9分)
=2×5.2=10.4(米)(10分)
答:树高AB约为5.2米,树影有最长值,最长值约为10.4米.(11分)
 解:(1)在Rt△ABC中,∠BAC=90°,∠C=30°
解:(1)在Rt△ABC中,∠BAC=90°,∠C=30°∵tanC=
| AB |
| AC |
∴AB=AC•tanC(3分)
=9×
| ||
| 3 |
≈5.2(米)(5分)
(2)以点A为圆心,以AB为半径作圆弧,当太阳光线与圆弧相切时树影最长,点D为切点,DE⊥AD交AC于E点,(如图)(7分)
在Rt△ADE中,∠ADE=90°,∠E=30°,
∴AE=2AD(9分)
=2×5.2=10.4(米)(10分)
答:树高AB约为5.2米,树影有最长值,最长值约为10.4米.(11分)
点评:此题主要是运用所学的解直角三角形的知识解决实际生活中的问题.分析以点A为圆心,以AB为半径作圆弧,当太阳光线与圆弧相切时树影最长,是解题的关键.

练习册系列答案
 阶梯计算系列答案
阶梯计算系列答案
相关题目
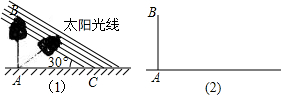 变化,假设太阳光线于地面夹角保持不变(用图(2)解答)
变化,假设太阳光线于地面夹角保持不变(用图(2)解答) ≈1.414,
≈1.414,  ≈1.732)
≈1.732)