题目内容
若△ABC∽△A′B′C′，相似比为
，且ABC的周长为21，△A'B'C'的面积为16，则△A′B′C′的周长为________，△ABC的面积为________．
14 36
分析：由△ABC∽△A′B′C′，相似比为，根据相似三角形的周长的比等于相似比，面积比等于相似比的平方，即可求得答案．
解答：∵△ABC∽△A′B′C′，相似比为，
∴△ABC与△A′B′C′的周长比为，面积比为
，
∵△ABC的周长为21，△A′B′C′的面积为16，
∴△A′B′C′的周长为14，△ABC的面积为36．
故答案为：14，36．
点评：此题考查了相似三角形的性质．此题比较简单，解题的关键是注意掌握相似三角形的周长的比等于相似比，面积比等于相似比的平方定理的应用．
分析：由△ABC∽△A′B′C′，相似比为
，根据相似三角形的周长的比等于相似比，面积比等于相似比的平方，即可求得答案．解答：∵△ABC∽△A′B′C′，相似比为
，∴△ABC与△A′B′C′的周长比为
，面积比为，∵△ABC的周长为21，△A′B′C′的面积为16，
∴△A′B′C′的周长为14，△ABC的面积为36．
故答案为：14，36．
点评：此题考查了相似三角形的性质．此题比较简单，解题的关键是注意掌握相似三角形的周长的比等于相似比，面积比等于相似比的平方定理的应用．
练习册系列答案
特高级教师点拨系列答案
相关题目
7、如图，D是线段AB，BC的垂直平分线的交点，若∠ABC=50°，则∠ADC的大小是（ ）
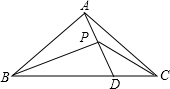如图，在等腰直角三角形ABC中，∠BAC=90°，在BC上截取BD=BA，作∠ABC的平分线与AD相交于点P，连结PC，若△ABC的面积为4cm2，则△BPC的面积为（ ）| A、4cm2 | B、3cm2 | C、2cm2 | D、8cm2 |