题目内容
在平面直角坐标系中，Rt△OAB的顶点A的坐标为
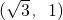，若将△OAB绕O点，逆时针旋转60°后，B点到达B′点，则点B′的坐标是________．
（
）
分析：根据A点坐标可知∠AOB=30°，因此旋转后OA在y轴上．如图所示．作B′C′⊥y轴于C′点，运用三角函数求出B′C′、OC′的长度即可确定B′的坐标．
解答：
解：将△OAB绕O点，逆时针旋转60°后，位置如图所示，
作B′C′⊥y轴于C′点，
∵A的坐标为，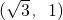
∴OB=
，AB=1，∠AOB=30°，
∴OB′=，∠B′OC′=30°，
∴B′C′=，OC′=
，
∴B′（，）．
点评：本题涉及图形旋转，体现了新课标的精神，抓住旋转的三要素：旋转中心O，旋转方向逆时针，旋转角度60°，通过画图计算得B′坐标．
）分析：根据A点坐标可知∠AOB=30°，因此旋转后OA在y轴上．如图所示．作B′C′⊥y轴于C′点，运用三角函数求出B′C′、OC′的长度即可确定B′的坐标．
解答：
解：将△OAB绕O点，逆时针旋转60°后，位置如图所示，作B′C′⊥y轴于C′点，
∵A的坐标为
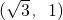，∴OB=
，AB=1，∠AOB=30°，∴OB′=
，∠B′OC′=30°，∴B′C′=
，OC′=，∴B′（
，）．点评：本题涉及图形旋转，体现了新课标的精神，抓住旋转的三要素：旋转中心O，旋转方向逆时针，旋转角度60°，通过画图计算得B′坐标．
练习册系列答案
相关题目
坐标原点．A、B两点的横坐标分别是方程x2-4x-12=0的两根，且cos∠DAB=
18、在平面直角坐标系中，把一个图形先绕着原点顺时针旋转的角度为θ，再以原点为位似中心，相似比为k得到一个新的图形，我们把这个过程记为【θ，k】变换．例如，把图中的△ABC先绕着原点O顺时针旋转的角度为90°，再以原点为位似中心，相似比为2得到一个新的图形△A1B1C1，可以把这个过程记为【90°，2】变换．