Question

（本小题满分10分）如图，已知反比例函数（）的图象与一次函数的图象交于两点，点的坐标为，连接平行于轴．

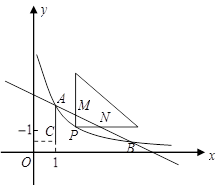
（1）求反比例函数的解析式及点的坐标．

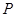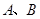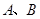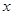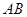（2）现有一个直角三角板，让它的直角顶点在反比例函数图象上的之间的部分滑动（不与重合），两直角边始终分别平行于轴、轴，且与线段交于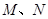两点，试判断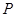点在滑动过程中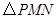是否与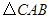总相似，简要说明判断理由．

 

Answer 1

解：（1）由得，代入反比例函数中，得

∴反比例函数解析式为：

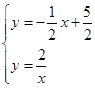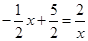解方程组由化简得：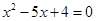

所以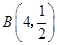

   （2）无论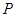点在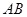之间怎样滑动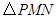，与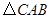总能相似．因为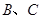两点纵坐标相等，所以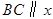轴．

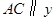又因为轴，所以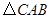为直角三角形．

同时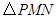也是直角三角形，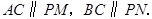

（在理由中只要能说出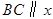轴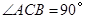，即可得分．）

解析:略