题目内容
把一副三角板放置在如图所示的位置，若把△DCE绕点C按逆时针方向旋转，旋转的角度为α（0°＜α＜180°），（1）若要使得DE∥AB，则α=
15
15
度；（2）若要使得△DCE中有一条边所在的直线与AB垂直，则α=
15或60或105
15或60或105
度．分析：（1）设CE与AB的交点为F，根据两直线平行，内错角相等可得∠BFE=∠E=45°，再根据三角形的一个外角等于与它不相邻的两个内角的和列式进行计算即可得解；
（2）分①CD⊥AB时，根据同位角相等两直线平行可得DE∥AB，根据（1）的结论解答即可；②CE⊥AB时，根据直角三角形两锐角互余列式求解即可；③DE⊥AB时，先根据直角三角形两锐角互余求出∠1，再根据三角形内角和定理列式进行计算即可得解．
（2）分①CD⊥AB时，根据同位角相等两直线平行可得DE∥AB，根据（1）的结论解答即可；②CE⊥AB时，根据直角三角形两锐角互余列式求解即可；③DE⊥AB时，先根据直角三角形两锐角互余求出∠1，再根据三角形内角和定理列式进行计算即可得解．
解答：
解：（1）如图，设CE与AB的交点为F，
∵DE∥AB，
∴∠BFE=∠E=45°，
∴∠α=∠BFE-∠B=45°-30°=15°；
（2）①CD⊥AB时，易得DE∥AB，
所以，α=15°；
②CE⊥AB时，如图1，α=90°-∠B=90°-30°=60°；
③DE⊥AB时，如图2，∠1=90°-∠E=90°-45°=45°，
所以，α=180°-∠1-∠B=180°-45°-30°=105°，
所以，α=15或60或105．
故答案为：15；．15或60或105．
解：（1）如图，设CE与AB的交点为F，∵DE∥AB，
∴∠BFE=∠E=45°，
∴∠α=∠BFE-∠B=45°-30°=15°；
（2）①CD⊥AB时，易得DE∥AB，
所以，α=15°；
②CE⊥AB时，如图1，α=90°-∠B=90°-30°=60°；
③DE⊥AB时，如图2，∠1=90°-∠E=90°-45°=45°，
所以，α=180°-∠1-∠B=180°-45°-30°=105°，
所以，α=15或60或105．
故答案为：15；．15或60或105．
点评：本题考查了旋转的性质，三角板的知识，熟悉三角板的度数是解题的关键，难点在于要分情况讨论．
练习册系列答案
名校课堂系列答案
相关题目
时点B在△D2CE2的内部，外部，还是边上？证明你的判断．
，
，
，斜边
，
．把三角板DCE绕点C顺时针旋转15°得到△D1CE1（如图乙）．这时AB与CD1相交于点
、与D1E1相交于点F．
的度数；（4分）
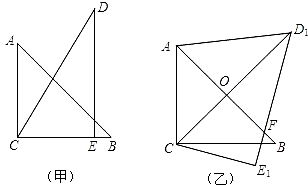
顺时针再旋转30°得△D2CE2，这时点B在△D2CE2的内部、外部、还是边上？请说明理由。（4分）把一副三角板如图甲放置，其中
，
，
，斜边
，
。把三角板DCE绕点C顺时针旋转15°得到△D1CE1（如图乙）。这时AB与CD1相交于点
，与D1E1相交于点F。
 |
1.（1）求
的度数；
2.（2）求线段AD1的长；
3.（3）若把三角形D1CE1绕着点
顺时针再旋转30°得△D2CE2，这时点B在△D2CE2的内部、外部、还是边上？说明理由。
把一副三角板放置在如图所示的位置，若把△DCE绕点C按逆时针方向旋转，旋转的角度为α（0°＜α＜180°），