题目内容
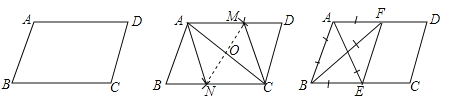
【题目】在
中，斜边AC的中点M关于BC的对称点O，将△ABC绕点O顺时针旋转至△DCE，连接BD，BE，如图所示.
(1)在①
，②
，③
中，等于旋转角的是 （填出满足条件的角的序号）；
(2)若
求
的大小（用含
的式子表示）；
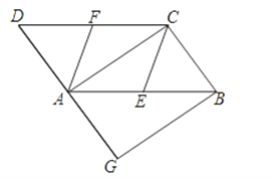
(3)点N是BD的中点，连接MN，用等式表示线段MN与BE之间的数量关系，并证明.
【答案】（1）③；(2) 
；（3）
.证明见解析.
【解析】试题分析：（1）根据旋转角的定义判断即可；
（2）连接
， 
， 
， 
，由直角三角形斜边上的中线等于斜边的一半，得
，由等边对等角得
，再由三角形外角的性质得
，由轴对称性质得
，由同弧所对的圆周角是圆心角的一半可证得
；
（3）连接
并延长到点
，使
，连接
.可证得四边形
是平行四边形，所以
，由三角形的中位线等于底边的一半，可证.
（1）③；
（2）连接
， 
， 
， 
，
∵
中， 
°，
为
的中点，
∴
，
∴
，
∵
= 
，
∴
，
∵点M和点O关于直线BC对称，
∴
.
∵
，
∴点C，B，E在以O为圆心， 
为半径的圆上，
∴
；
（3）
.证明如下：
连接
并延长到点
，使
，连接
.
∵
°，
∴
°-
°
，
∴
°
，
∵
，
∴
°，
∵
，
∴
，
∵
，
∴
°
，
∴
°，
∴
°，
∴
∥
，
∵
，
∴
，
∴四边形
是平行四边形.
∴
，
∵
，
∴
，
∴
.
练习册系列答案
优等生题库系列答案
相关题目
