题目内容
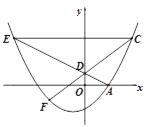
【题目】如图，抛物线
与x轴正半轴交于点A，点D（0，m）为y轴正半轴上一点，连结AD并延长交抛物线于点E. 若点C（4，n）在抛物线上，且CE∥x轴.
（1）求m，n的值.
（2）连结CD并延长交抛物线于点F，求
的值.
【答案】（1）m=1，n=4；（2）
【解析】（1）∵点C（4，n）在抛物线上，∴x=4，代入抛物线得，n=4
令y=0，得
， 解得
∴A（2,0）
∵CE∥x轴，∴将y=4代入
，得
解得
∴E（-6,4）， 求得直线EC的解析式为
当x=0时，y=1,∴m=1
（或作EG⊥x轴，得
，∴m=1 ）
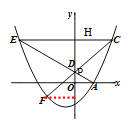
（2）作FP⊥y轴于P，
设直线CD的解析式为
将C（4,4），D（0,1）代入上式得
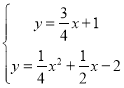解得
解得， 
∴
∵CE∥FP，∴ 
∴ 
练习册系列答案
长江作业本同步练习册系列答案
小天才课时作业系列答案
相关题目
