题目内容
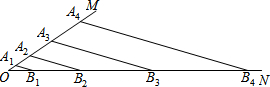 如图,点A1、A2、A3、…,点B1、B2、B3、…,分别在射线OM、ON上,A1B1∥A2B2∥A3B3∥A4B4∥….如果A1B1=2,A1A2=2OA1,A2A3=3OA1,A3A4=4OA1,….那么A2B2=
如图,点A1、A2、A3、…,点B1、B2、B3、…,分别在射线OM、ON上,A1B1∥A2B2∥A3B3∥A4B4∥….如果A1B1=2,A1A2=2OA1,A2A3=3OA1,A3A4=4OA1,….那么A2B2=6
6
,AnBn=n(n+1)
n(n+1)
.(n为正整数)分析:根据OA1=1,求出A1A2、A2A3、A3A4的值,推出AnAn-1的值,根据平行线分线段成比例定理得出
=
,代入求出A2B2=6=2×(2+1),A3B3=12=3×(3+1),A4B4=20=4(4+1),推出AnBn=n(n+1)即可.
| OA1 |
| OA2 |
| A1B1 |
| A2B2 |
解答:解:∵OA1=1,
∴A1A2=2×1=2,
A2A3=3×1=3,
A3A4=4,
…
An-2An-1=n-1,
An-1An=n,
∵A1B1∥A2B2∥A3B3∥A4B4∥…,
∴
=
,
∴
=
,
∴A2B2=6=2×(2+1),
A3B3=12=3×(3+1),
A4B4=20=4(4+1),
…,
∴AnBn=n(n+1),
故答案为:6,n(n+1).
∴A1A2=2×1=2,
A2A3=3×1=3,
A3A4=4,
…
An-2An-1=n-1,
An-1An=n,
∵A1B1∥A2B2∥A3B3∥A4B4∥…,
∴
| OA1 |
| OA2 |
| A1B1 |
| A2B2 |
∴
| 1 |
| 1+2 |
| 2×1 |
| A2B2 |
∴A2B2=6=2×(2+1),
A3B3=12=3×(3+1),
A4B4=20=4(4+1),
…,
∴AnBn=n(n+1),
故答案为:6,n(n+1).
点评:本题考查了平行线分线段成比例定理的应用,解此题的关键是根据求出的结果得出规律,题型较好,但是有一定的难度.

练习册系列答案
 直通贵州名校周测月考直通名校系列答案
直通贵州名校周测月考直通名校系列答案
相关题目
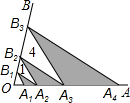 如图,点A1,A2,A3,A4在射线OA上,点B1,B2,B3在射线OB上,且A1B1∥A2B2∥A3B3,A2B1∥A3B2∥A4B3.若△A2B1B2,△A3B2B3的面积分别为1,4,则图中三个阴影三角形面积之和为
如图,点A1,A2,A3,A4在射线OA上,点B1,B2,B3在射线OB上,且A1B1∥A2B2∥A3B3,A2B1∥A3B2∥A4B3.若△A2B1B2,△A3B2B3的面积分别为1,4,则图中三个阴影三角形面积之和为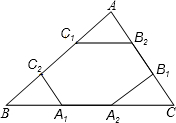 如图,点A1、A2,B1、B2,C1、C2分别是△ABC的边BC、CA、AB的三等分点,若△ABC的周长为L,则六边形A1A2B1B2C1C2的周长为( )
如图,点A1、A2,B1、B2,C1、C2分别是△ABC的边BC、CA、AB的三等分点,若△ABC的周长为L,则六边形A1A2B1B2C1C2的周长为( )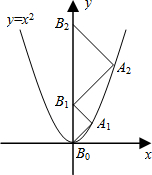 如图,点A1、A2、A3、…、An在抛物线y=x2图象点B1、B2、B3、…、Bn在y轴上,若△A1B0B1、△A2B1B2、…、△AnBn-1Bn都为等腰直角三角形(点B0是坐标原点),则△A2012B2011B2012的腰长=
如图,点A1、A2、A3、…、An在抛物线y=x2图象点B1、B2、B3、…、Bn在y轴上,若△A1B0B1、△A2B1B2、…、△AnBn-1Bn都为等腰直角三角形(点B0是坐标原点),则△A2012B2011B2012的腰长= (2013•南京二模)如图,点A1、A2、A3、A4、A5在⊙O上,且
(2013•南京二模)如图,点A1、A2、A3、A4、A5在⊙O上,且