题目内容
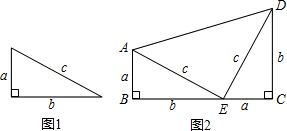
在直角梯形中，一底与一腰的夹角为45°，并且这腰的长为4cm，则另一腰的长为分析：如图作DE⊥BC于E点，根据∠DCE=45°，DC=4可以求得DE的长，则DE的长就是AB的长．
解答：
解：作DE⊥BC于E点，
∵梯形ABCD是直角梯形，
∴DE=AB，
∵∠DCE=45°，DC=4，
∴AB=DE=2
，
故答案为2
．
解：作DE⊥BC于E点，∵梯形ABCD是直角梯形，
∴DE=AB，
∵∠DCE=45°，DC=4，
∴AB=DE=2
| 2 |
故答案为2
| 2 |
点评：此题考查了直角梯形中常用的计算问题．所作辅助线是直角梯形中常作辅助线，把直角梯形转化为矩形和直角三角形后求解．
练习册系列答案
相关题目
，则梯形的面积为________cm2．