题目内容
24、如图，ABCD为正方形，请在平面内找出点P，使得PAB、PBC、PCD、PDA都是等腰三角形，并指出这样的点有几个，在图中作出这样的点P．分析：以AB，CD的中点连线为x轴，BC，AD的中点连线为y轴，原点P1使得PAB、PBC、PCD、PDA都是等腰三角形明显易证明，以A为圆心，AD为半径可得P7，P3，P9，P5，以C为圆心，CD为半径可得P2，P6，P4，P8，共9个．
解答：解：如图，以AB，CD的中点连线为x轴，BC，AD的中点连线为y轴，
原点P1使得PAB、PBC、PCD、PDA都是等腰三角形明显易证明，
以A为圆心，AD为半径可得P7，P3，P9，P5，
以C为圆心，CD为半径可得P2，P6，P4，P8，共9个．
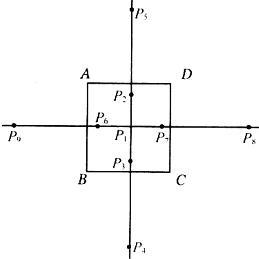
原点P1使得PAB、PBC、PCD、PDA都是等腰三角形明显易证明，
以A为圆心，AD为半径可得P7，P3，P9，P5，
以C为圆心，CD为半径可得P2，P6，P4，P8，共9个．
点评：解答本题要充分利用正方形的特殊性质．注意在正方形中的等腰三角形的作图办法．
练习册系列答案
相关题目
24、如图，在正方ABCD中，E是AB边上任一点，BG⊥CE，垂足为O，交AC于点F，交AD于点G．
)，直线AE与CD交于E,DE=6。以BE为折痕，把点A翻恰好与点C重合；动点P从点D出发沿着D→C→B→O路径匀速运动，速度为每秒4个单位；以P为圆心的⊙P半径每秒增加
个单位，当点P在点D处时，⊙P半径为
个单位；直线AE、⊙P同时出发，当点P到终点O时两者都停止，运动时间为t;
)，直线AE与CD交于E,DE=6。以BE为折痕，把点A翻恰好与点C重合；动点P从点D出发沿着D→C→B→O路径匀速运动，速度为每秒4个单位；以P为圆心的⊙P半径每秒增加
个单位，当点P在点D处时，⊙P半径为
个单位；直线AE、⊙P同时出发，当点P到终点O时两者都停止，运动时间为t;
