题目内容
如图，已知点A（3，4），点B为直线x=-1上的动点，设B（-1，y）．点C（x，0）且-1＜x＜3，BC⊥AC，则y与x之间的函数关系式________．
y=
x2+
x+
分析：过点A作AE⊥x轴于点E，证得△BCD与△CAE相似，
解答：如图，
过点A作AE⊥x轴于点E．在△BCD与△CAE中，
∵∠BCD=∠CAE=90°-∠ACE，∠BDC=∠CEA=90°，
∴△BCD∽△CAE，
∴BD：CE=CD：AE，
∵A（3，4），B（-1，y），C（x，0）且-1＜x＜3，
∴y：（3-x）=（x+1）：4，
∴y=x2+x+．
故答案为：y=x2+x+．
点评：此题利用三角形相似的判定与性质，来解决二次函数解析式的问题．
x2+x+分析：过点A作AE⊥x轴于点E，证得△BCD与△CAE相似，
解答：如图，
过点A作AE⊥x轴于点E．在△BCD与△CAE中，
∵∠BCD=∠CAE=90°-∠ACE，∠BDC=∠CEA=90°，
∴△BCD∽△CAE，
∴BD：CE=CD：AE，
∵A（3，4），B（-1，y），C（x，0）且-1＜x＜3，
∴y：（3-x）=（x+1）：4，
∴y=
x2+x+．故答案为：y=
x2+x+．点评：此题利用三角形相似的判定与性质，来解决二次函数解析式的问题．
练习册系列答案
相关题目
16、如图，已知点D是∠ABC的平分线上一点，点P在BD上，PA⊥AB，PC⊥BC，垂足分别为A，C、下列结论错误的是（ ）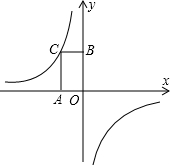
如图，已知点C为反比例函数y=-
如图，已知点A、B、C、D均在已知圆上，AD∥BC，AC平分∠BCD，∠ADC=120°，四边形ABCD的周长为10cm．图中阴影部分的面积为（ ）A、
| ||||
B、
| ||||
C、2
| ||||
D、4
|
如图，已知点D为△ABC中AC边上一点，且AD：DC=3；4，设
如图，已知点C为AB上一点，AC=12cm，CB=