Question

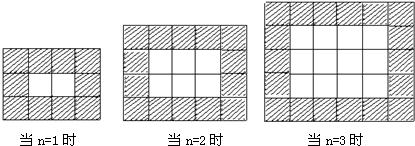
12、如图，用同样规格的黑白两色的正方形瓷砖铺设矩形地面，请你观察下列图形并解答问题：在第n个图形中，每-横行共有白色瓷砖

（n+1）

块，每-竖列共有白色瓷砖

n

块，整个图形共有

（n+3）（n+2）或（n²+5n+6）

块瓷砖．（均用含n的代数式表示）

Answer 1

分析：此题显然按照长方形的周长=长×宽计算，较为简便．

解答：解：白色瓷砖：第一个横行是2个，竖列是1个，第二个横行是3个，竖列是2个，推而广之，第n个横行是（n+1）个，竖列是n个．
整个图形的第n个图形中，横行是（n+3）个，竖列是（n+2）个，共有（n+3）（n+2）个，即（n²+5n+6）个．

点评：算此类题中的图形个数时，注意运用长方形的周长公式．