题目内容
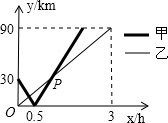
在一条直线上依次有A、B、C三个港口,甲、乙两船同时分别从A、B港口出发,沿直线匀速驶向C港,最终达到C港.设甲、乙两船行驶x(h)后,与B港的距离分别为y1、y2(km),y1、y2与x的函数关系如图所示。
(1)填空:A、C两港口间的距离为( )km,a=( );
(2)求图中点P的坐标,并解释该点坐标所表示的实际意义;
(3)若两船的距离不超过10km时能够相互望见,求甲、乙两船可以相互望见时x的取值范围。
(1)填空:A、C两港口间的距离为( )km,a=( );
(2)求图中点P的坐标,并解释该点坐标所表示的实际意义;
(3)若两船的距离不超过10km时能够相互望见,求甲、乙两船可以相互望见时x的取值范围。

解:(1)120;2;
(2)由点(3,90)求得,y2=30x,
当x>0.5时,由点(0.5,0),(2,90)求得,
y1=60x﹣30,
当y1=y2时,60x﹣30=30x,
解得,x=1,
此时y1=y2=30,
所以点P的坐标为(1,30),
该点坐标的意义为:两船出发1h后,甲船追上乙船,此时两船离B港的距离为30km;
(3)①当x≤0.5时,由点(0,30),(0.5,0)求得,
y1=﹣60x+30
依题意,(﹣60x+30)+30x≤10.解得,x≥ 不合题意;
不合题意;
②当0.5<x≤1时,依题意,30x﹣(60x﹣30)≤10
解得,x≥ ,
,
所以 ≤x≤1;
≤x≤1;
③当x>1时,依题意,(60x﹣30)﹣30x≤10
解得,x≤
所以1<x≤ ;
;
④当2≤x≤3时,甲船已经到了而乙船正在行驶,
∵90﹣30x≤10,解得x≥ ,
,
所以,当 ≤x≤3,甲、乙两船可以相互望见;
≤x≤3,甲、乙两船可以相互望见;
综上所述,当 ≤x≤
≤x≤ 时或当
时或当 ≤x≤3时,甲、乙两船可以相互望见。
≤x≤3时,甲、乙两船可以相互望见。
(2)由点(3,90)求得,y2=30x,
当x>0.5时,由点(0.5,0),(2,90)求得,
y1=60x﹣30,
当y1=y2时,60x﹣30=30x,
解得,x=1,
此时y1=y2=30,
所以点P的坐标为(1,30),
该点坐标的意义为:两船出发1h后,甲船追上乙船,此时两船离B港的距离为30km;
(3)①当x≤0.5时,由点(0,30),(0.5,0)求得,
y1=﹣60x+30
依题意,(﹣60x+30)+30x≤10.解得,x≥
 不合题意;
不合题意;②当0.5<x≤1时,依题意,30x﹣(60x﹣30)≤10
解得,x≥
 ,
,所以
 ≤x≤1;
≤x≤1;③当x>1时,依题意,(60x﹣30)﹣30x≤10
解得,x≤

所以1<x≤
 ;
;④当2≤x≤3时,甲船已经到了而乙船正在行驶,
∵90﹣30x≤10,解得x≥
 ,
,所以,当
 ≤x≤3,甲、乙两船可以相互望见;
≤x≤3,甲、乙两船可以相互望见;综上所述,当
 ≤x≤
≤x≤ 时或当
时或当 ≤x≤3时,甲、乙两船可以相互望见。
≤x≤3时,甲、乙两船可以相互望见。
练习册系列答案
相关题目
 在一条直线上依次有A、B、C三个港口,甲、乙两船同时分别从A、B港口出发,沿直线匀速驶向C港,最终达到C港.设甲、乙两船行驶x(h)后,与B港的距离分别为y1、y2(km),y1、y2与x的函数关系如图所示.若两船的距离为10km时,甲行驶了
在一条直线上依次有A、B、C三个港口,甲、乙两船同时分别从A、B港口出发,沿直线匀速驶向C港,最终达到C港.设甲、乙两船行驶x(h)后,与B港的距离分别为y1、y2(km),y1、y2与x的函数关系如图所示.若两船的距离为10km时,甲行驶了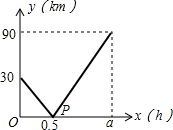 (2013•溧水县一模)在一条直线上依次有A、B、C三个海岛,某海巡船从A岛出发沿直线匀速经B岛驶向C岛,执行海巡任务,最终达到C岛.设该海巡船行驶x(h)后,与B港的距离为y(km),y与x的函数关系如图所示.
(2013•溧水县一模)在一条直线上依次有A、B、C三个海岛,某海巡船从A岛出发沿直线匀速经B岛驶向C岛,执行海巡任务,最终达到C岛.设该海巡船行驶x(h)后,与B港的距离为y(km),y与x的函数关系如图所示. (2013•滨湖区二模)在一条直线上依次有A、B、C三个海岛,某海巡船从A岛出发沿直线匀速经B 岛驶向C岛,执行海巡任务,最终达到C岛.设该海巡船行驶x(h)后,与B港的距离为y(km),y与x的函数关系如图所示.
(2013•滨湖区二模)在一条直线上依次有A、B、C三个海岛,某海巡船从A岛出发沿直线匀速经B 岛驶向C岛,执行海巡任务,最终达到C岛.设该海巡船行驶x(h)后,与B港的距离为y(km),y与x的函数关系如图所示. 终达到C港.设甲、乙两船行驶x(h)后,与B港的距离分别为y1、y2(km),y1、y2与x的函数关系如图所示.
终达到C港.设甲、乙两船行驶x(h)后,与B港的距离分别为y1、y2(km),y1、y2与x的函数关系如图所示.