题目内容
设x1、x2为方程2x2-mx+m=0的两个实数根，且x12+x22=3，求m的值．
解：由题意可知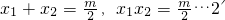
，
∵x12+x22=（x1+x2）2-2x1x2…4'，
∴
，
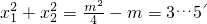m1=6，m2=-2…7'，
当m1=6时，△＜0，
所以m=-2．…8'
分析：由于x12+x22=（x1+x2）2-2x1x2，根据根与系数的关系（x1+x2=-
，x1•x2=
）解得．
点评：本题考查了一元二次方程ax2+bx+c=0（a≠0）的根与系数的关系，本题转化了形势，需要考生灵活把代数转化为根与系数关系的形势来求．
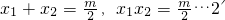，∵x12+x22=（x1+x2）2-2x1x2…4'，
∴
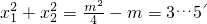，m1=6，m2=-2…7'，
当m1=6时，△＜0，
所以m=-2．…8'
分析：由于x12+x22=（x1+x2）2-2x1x2，根据根与系数的关系（x1+x2=-
，x1•x2=）解得．点评：本题考查了一元二次方程ax2+bx+c=0（a≠0）的根与系数的关系，本题转化了形势，需要考生灵活把代数转化为根与系数关系的形势来求．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
已知关于x的一元二次方程x2-6x-k2=0（k为常数）．