题目内容
分别在坐标系中画出它们的函数图象.
(1)y= ;
;
(2)y=﹣ .
.
见解析
解析试题分析:(1)根据反比例函数的性质得出2xy=1,进而得出点的坐标,即可得出答案;
(2)根据反比例函数的性质得出xy=﹣3,进而得出点的坐标,即可得出答案.
解:(1)如图所示:
列表得出:
x ﹣2 ﹣1 ﹣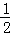 ﹣
﹣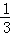
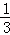
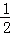 1 2
1 2
y ﹣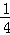 ﹣
﹣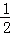 ﹣1 ﹣
﹣1 ﹣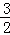
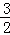 1
1 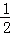
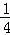
(2)如图所示:
x ﹣5 ﹣4 ﹣3 ﹣2 ﹣1 1 2 3 4 5
y 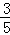
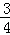 1
1 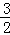 3 ﹣3 ﹣
3 ﹣3 ﹣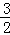 ﹣1 ﹣
﹣1 ﹣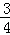 ﹣
﹣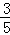
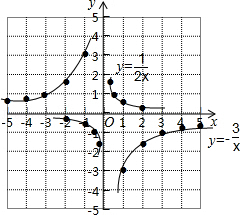
考点:反比例函数的图象.
点评:此题主要考查了画反比例函数的图象,根据反比例函数的性质得出点的坐标性质进而得出是解题关键.

练习册系列答案
 桃李文化快乐暑假武汉出版社系列答案
桃李文化快乐暑假武汉出版社系列答案 优秀生快乐假期每一天全新寒假作业本系列答案
优秀生快乐假期每一天全新寒假作业本系列答案
相关题目
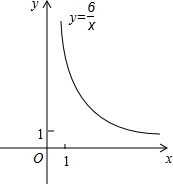 如图,平面直角坐标系xOy中,点pn(xn,yn)在双曲线
如图,平面直角坐标系xOy中,点pn(xn,yn)在双曲线 上(n,xn,yn都是正整数,且x1<x2<x3<…<xn).抛物线y=ax2+bx+c经过(0,3),(-2,3),(1,0)三点.
上(n,xn,yn都是正整数,且x1<x2<x3<…<xn).抛物线y=ax2+bx+c经过(0,3),(-2,3),(1,0)三点.
| x | … | … | |||||
| y | … | … |
(2)直接写出点pn(xn,yn)的坐标,并写出pn中任意两点所确定的不同直线的条数;
(3)从(2)中得到的所有直线中随机(任意)取出一条,利用图象求取出的直线与抛物线有公共点的概率;
(4)设抛物线y=ax2+bx+c与x轴的交点分别为A,B(A在B左侧),将抛物线y=ax2+bx+c向上平移,平移后的抛物线与x轴的交点分别记为C,D(C在D左侧),求
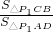 值.
值.
如图,平面直角坐标系xOy中,点pn(xn,yn)在双曲线 上(n,xn,yn都是正整数,且x1<x2<x3<…<xn).抛物线y=ax2+bx+c经过(0,3),(-2,3),(1,0)三点.
上(n,xn,yn都是正整数,且x1<x2<x3<…<xn).抛物线y=ax2+bx+c经过(0,3),(-2,3),(1,0)三点.
(1)求抛物线y=ax2+bx+c的解析式并在坐标系中画出它的图象;
(2)直接写出点pn(xn,yn)的坐标,并写出pn中任意两点所确定的不同直线的条数;
(3)从(2)中得到的所有直线中随机(任意)取出一条,利用图象求取出的直线与抛物线有公共点的概率;
(4)设抛物线y=ax2+bx+c与x轴的交点分别为A,B(A在B左侧),将抛物线y=ax2+bx+c向上平移,平移后的抛物线与x轴的交点分别记为C,D(C在D左侧),求 值.
值.

 上(n,xn,yn都是正整数,且x1<x2<x3<…<xn).抛物线y=ax2+bx+c经过(0,3),(-2,3),(1,0)三点.
上(n,xn,yn都是正整数,且x1<x2<x3<…<xn).抛物线y=ax2+bx+c经过(0,3),(-2,3),(1,0)三点. | x | … | … | |||||
| y | … | … |
(2)直接写出点pn(xn,yn)的坐标,并写出pn中任意两点所确定的不同直线的条数;
(3)从(2)中得到的所有直线中随机(任意)取出一条,利用图象求取出的直线与抛物线有公共点的概率;
(4)设抛物线y=ax2+bx+c与x轴的交点分别为A,B(A在B左侧),将抛物线y=ax2+bx+c向上平移,平移后的抛物线与x轴的交点分别记为C,D(C在D左侧),求
 值.
值.
 (2011•西城区模拟)如图,平面直角坐标系xOy中,点pn(xn,yn)在双曲线
(2011•西城区模拟)如图,平面直角坐标系xOy中,点pn(xn,yn)在双曲线