题目内容
如图，E、F分别是?ABCD的边AD、BC上的点，且AE=CF，AF和BE相交于点G，DF和CE相交于点H，求证：EF和GH互相平分．分析：可先证明四边形AFCE是平行四边形，进而利用平行四边形的性质得出四边形GFHE是平行四边形，即可得出结论．
解答：证明：∵E为AD的中点，F为BC的中点，
∴AE=
AD，CF=
BC，
∵四边形ABCD是平行四边形，
∴AD∥BC，
∴AE∥CF，AE=CF，
∴四边形AFCE是平行四边形，
∴AF∥CE，
同理可证：BE∥DF，
∴四边形GFHE是平行四边形，
∴EF与GH互相平分．
∴AE=
| 1 |
| 2 |
| 1 |
| 2 |
∵四边形ABCD是平行四边形，
∴AD∥BC，
∴AE∥CF，AE=CF，
∴四边形AFCE是平行四边形，
∴AF∥CE，
同理可证：BE∥DF，
∴四边形GFHE是平行四边形，
∴EF与GH互相平分．
点评：本题主要考查平行四边形的判定问题，能够熟练掌握并求解此类问题．
练习册系列答案
相关题目
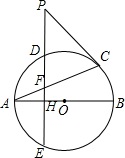如图：AB、AC分别是⊙O的直径和弦，D为弧AC上一点，DE⊥AB于点H，交⊙O于点E，交AC于点F．P为ED延长线上一点，连PC．
如图，AB和AC分别是⊙O的直径和弦，OD⊥AC于D点，若OA=4，∠A=30°，则BD等于（ ）
已知：如图，E、F分别是正方形ABCD边BC、AD上的点，且BE=DF
桌上放着一个圆柱和一个长方体，如图（1），请说出下列三幅图（如图（2））分别是从哪个方向看到的．