题目内容
（2013•株洲）已知a、b可以取-2、-1、1、2中任意一个值（a≠b），则直线y=ax+b的图象不经过第四象限的概率是
．
| 1 |
| 6 |
| 1 |
| 6 |
分析：列表得出所有等可能的结果数，找出a与b都为正数，即为直线y=ax+b不经过第四象限的情况数，即可求出所求的概率．
解答：解：列表如下：
所有等可能的情况数有12种，其中直线y=ax+b不经过第四象限情况数有2种，
则P=
=
．
故答案为：
| -2 | -1 | 1 | 2 | |
| -2 | （-1，-2） | （1，-2） | （2，-2） | |
| -1 | （-2，-1） | （1，-1） | （2，-1） | |
| 1 | （-2，1） | （-1，1） | （2，1） | |
| 2 | （-2，2） | （-1，2） | （1，2） |
则P=
| 2 |
| 12 |
| 1 |
| 6 |
故答案为：
| 1 |
| 6 |
点评：此题考查了列表法与树状图法，以及一次函数图象与系数的关系，用到的知识点为：概率=所求情况数与总情况数之比．
练习册系列答案
阅读快车系列答案
相关题目
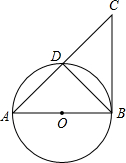（2013•株洲）已知AB是⊙O的直径，直线BC与⊙O相切于点B，∠ABC的平分线BD交⊙O于点D，AD的延长线交BC于点C．
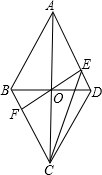（2013•株洲）已知四边形ABCD是边长为2的菱形，∠BAD=60°，对角线AC与BD交于点O，过点O的直线EF交AD于点E，交BC于点F．
（2013•株洲）已知抛物线C1的顶点为P（1，0），且过点（0，