题目内容
(2010•普陀区一模)如图,已知CE是Rt△ABC斜边AB上的高,在EC的延长线上任取一点P,连接AP,BG⊥AP垂足为G,交CE于D,求证:CE2=PE•DE.

【答案】分析:首先证Rt△ACE∽Rt△CBE,得出CE2=AE•BE(即射影定理);再通过证△AEP∽△BED,得出PE•DE=AE•BE,联立上述两式即可得出本题要证的结论.
解答: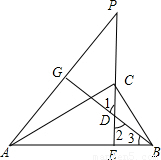 证明:
证明:
∵∠ACB=90°,CE⊥AB,
∴∠ACE+∠BCE=90°,∠ACE+∠CAE=90°,
∴∠CAE=∠BCE,
∴Rt△ACE∽Rt△CBE;(1分)
∴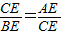 ;(1分)
;(1分)
∴CE2=AE•BE;(1分)
又∵BG⊥AP,CE⊥AB,
∴∠DEB=∠DGP=∠PEA=90°,(1分)
∵∠1=∠2,
∴∠P=∠3(1分)
∴△AEP∽△DEB (1分)
∴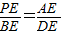 (1分)
(1分)
∴PE•DE=AE•BE(1分)
∴CE2=PE•DE.(1分)
点评:此题主要考查的是相似三角形的判定和性质.
解答:
 证明:
证明:∵∠ACB=90°,CE⊥AB,
∴∠ACE+∠BCE=90°,∠ACE+∠CAE=90°,
∴∠CAE=∠BCE,
∴Rt△ACE∽Rt△CBE;(1分)
∴
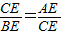 ;(1分)
;(1分)∴CE2=AE•BE;(1分)
又∵BG⊥AP,CE⊥AB,
∴∠DEB=∠DGP=∠PEA=90°,(1分)
∵∠1=∠2,
∴∠P=∠3(1分)
∴△AEP∽△DEB (1分)
∴
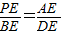 (1分)
(1分)∴PE•DE=AE•BE(1分)
∴CE2=PE•DE.(1分)
点评:此题主要考查的是相似三角形的判定和性质.

练习册系列答案
 出彩同步大试卷系列答案
出彩同步大试卷系列答案
相关题目


