Question

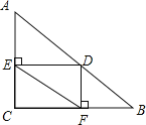
【题目】如图，在△ABC中，AB=10，BC=8，AC=6．点D在AB边上(不包括端点)，DE⊥AC，DF⊥BC，垂足分别为点E和点F，连结EF．

(1)判断四边形DECF的形状，并证明；

(2)线段EF是否存在最小值？如果存在，请求出最小值；如果不存在，请说明理由．

Answer 1

【答案】（1）四边形DECF是矩形，理由见解析；（2）存在，EF=4.8．

【解析】

(1)根据勾股定理的逆定理得到△ABC是直角三角形，∠C=90°，由垂直的定义得到∠DEC=DFC=90°，于是得到四边形DECF是矩形；

(2)连结CD，由矩形的性质得到CD=EF，当CD⊥AB时，CD取得最小值，即EF为最小值，根据三角形的面积即可得到结论．

解：(1)四边形DECF是矩形，

理由：∵在△ABC中，AB=10，BC=8，AC=6，

∴BC2+AC2=82+62=102=AB2，

∴△ABC是直角三角形，∠C=90°，

∵DE⊥AC，DF⊥BC，

∴∠DEC=DFC=90°，

∴四边形DECF是矩形；

(2)存在，连结CD，

∵四边形DECF是矩形，

∴CD=EF，

当CD⊥AB时，CD取得最小值，即EF为最小值，

∵S△ABC=ABCD=ACBC，

∴10×CD=6×8，

∴EF=CD=．